树形结构

2024/4/8大约 41 分钟

树形结构

概述

基本概念

节点、根节点、父节点、子节点、兄弟节点(有相同的父节点)
一棵树可以没有任何节点，称为 空树
一棵树可以只有 1 个节点，也就是 只有根节点
子树、左子树、右子树
节点的度（degree）：子树的个数
树的度：所有节点度中的最大值
叶子节点（leaf）：度为 0 的节点
非叶子节点：度不为 0 的节点
层数（level）：根节点在第 1 层，根节点的子节点在第 2 层，以此类推（有些说法也从第 0 层开始计算）
节点的深度（depth）：从根节点到当前节点的唯一路径上的节点总数
节点的高度（height）：从当前节点到最远叶子节点的路径上的节点总数
树的深度：所有节点深度中的最大值
树的高度：所有节点高度中的最大值
树的深度 等于 树的高度
树支路总数 = 树节点总数 - 1 (树中每个节点头上都有一个支路，但唯独根节点没有)

有序树，无序树，森林

有序树：树中任意节点的子节点之间有顺序关系
无序树：树中任意节点的子节点之间没有顺序关系，也称为“自由树”
森林：由 m（m ≥ 0）棵互不相交的树组成的集合

二叉树

特点

每个节点的度最大为 2（最多拥有 2 棵子树）
左子树和右子树是有顺序的
即使某节点只有一棵子树，也要区分左右子树
二叉树是度不大于2的有序树。但是度不大于2的有序树不是二叉树(因为有序树的节点次序是相对于另一节点而言的，当有序树的子树中只有一个孩子时，这个孩子节点无需区分左右次序，而二叉树无论孩子树是否为2，均需要确定左右次序）。

性质

非空二叉树的第 i 层，最多有 2^( i − 1) 个节点（ i ≥ 1 ）
在高度为 h 的二叉树上最多有 2^h − 1 个结点（ h ≥ 1 ）

// S=2^0 + 2^1 + 2^2 + 2^3 +..+ 2^(n-1)
// 2S=2^1 + 2^2 + 2^3 +..+ 2^(n-1) + 2^n
// 两式相减
// 2S-S=2^n - 2^0
// S=2^n - 1

对于任何一棵非空二叉树，如果叶子节点个数为 n0，度为 2 的节点个数为 n2，则有: n0 = n2 + 1

//推导步骤：
// ① 假设度为 1 的节点个数为 n1，那么二叉树的节点总数 n = n0 + n1 + n2 
// ② 二叉树的支路数 T = n1 + 2 * n2 = n – 1 = n0 + n1 + n2 – 1 
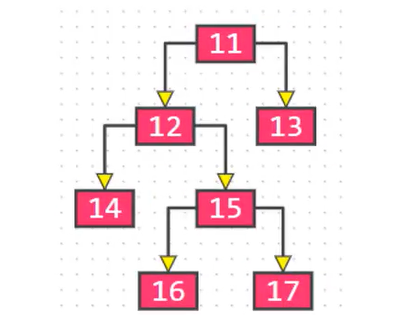
// ③ 因此 n0 = n2 + 1

真二叉树

理解：所有节点的度都要么为 0，要么为 2。

满二叉树

理解：最后一层节点的度都为 0，其他节点的度都为 2。

注意：
① 在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多。
② 满二叉树一定是真二叉树，真二叉树不一定是满二叉树。

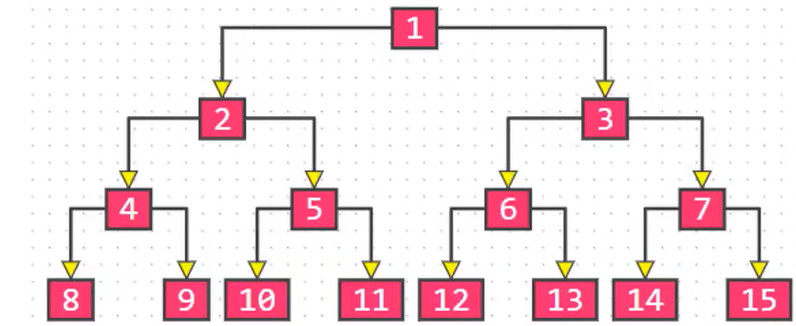
完全二叉树

理解：对节点从上至下、左至右开始编号，其所有编号都能与相同高度的满二叉树中的编号对应。

注意：
① 叶子节点只会出现最后 2 层，最后 1 层的叶子结点都靠左对齐。
② 完全二叉树从根结点至倒数第 2 层是一棵满二叉树。
③ 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

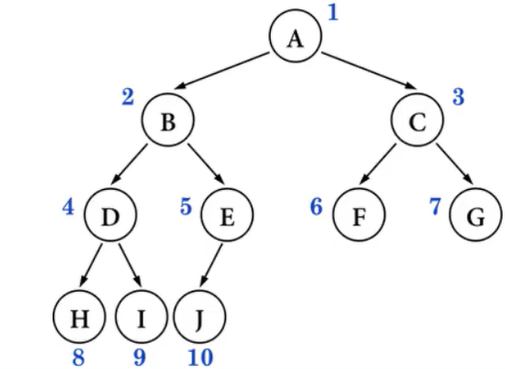
性质：

// 1. 度为 1 的节点只有左子树。
// 2. 度为 1 的节点要么是 1 个，要么是 0 个
// 3. 同样节点数量的二叉树，完全二叉树的高度最小
// 4. 假设完全二叉树的高度为 h（h ≥ 1），那么：
//    ① 至少有 2^(h−1) 个节点 （2^0 + 2^1 + 2^2 + ⋯ + 2^(h−2) + 1 ）
//    ② 最多有 2^h − 1 个节点（2^0 + 2^1 + 2^2 + ⋯ + 2^(h−1)，满二叉树）
//    ③ 当总节点数量为 n，
//      可得：2^(h-1) <= n < 2^h
//     =》   h - 1 <= logn < h
//     =》   h = floor(logn) + 1  ※  //floor:向下取整 ceiling：向上取整
// 5. 一棵有 n 个节点的完全二叉树（n > 0），从上到下、从左到右对节点从 1 开始
//    进行编号，对任意第 i 个节点：
//    ① 如果 i = 1 ，它是根节点
//    ② 如果 i > 1 ，它的父节点编号为 floor( i / 2 )
//    ③ 如果 2i ≤ n ，它的左子节点编号为 2i
//    ④ 如果 2i > n ，它无左子节点
//    ⑤ 如果 2i + 1 ≤ n ，它的右子节点编号为 2i + 1
//    ⑥ 如果 2i + 1 > n ，它无右子节点
// 6. 一棵有 n 个节点的完全二叉树（n > 0），从上到下、从左到右对节点从 0 
//   开始进行编号，对任意第 i 个节点：
//   ① 如果 i = 0 ，它是根节点
//   ② 如果 i > 0 ，它的父节点编号为 floor( (i – 1) / 2 )
//   ③ 如果 2i + 1 ≤ n – 1 ，它的左子节点编号为 2i + 1
//   ④ 如果 2i + 1 > n – 1 ，它无左子节点
//   ⑤ 如果 2i + 2 ≤ n – 1 ，它的右子节点编号为 2i + 2
//   ⑥ 如果 2i + 2 > n – 1 ，它无右子节点

面试题：如果一棵完全二叉树有 768 个节点，求叶子节点的个数

// 解： 设叶子节点为 n0，度为2的节点为 n2，度为1的节点为 n1
//     n = n0 + n1 + n2
//     n0 = n2 + 1
//     => n = 2n0 + n1 - 1
// 又因 完全二叉树度为1的节点要么是 1 个，要么是 0 个
//     ① n1为1 时，n = 2n0，n必然为偶数。
//     ② n1为0时，n = 2n0 - 1,n必然为奇数。
//     => n0 = 768 / 2 = 384

由以上题总结公式：

当总节点为偶数，n0 = n / 2。
当总节点数为奇数，n0 = (n + 1) / 2
=> n0 = floor( (n + 1) / 2 ) = ceiling( n / 2) 注意：java除法默认向下取整

判断一棵树是否为完全二叉树：

思路一：

思路二：

二叉树的遍历

遍历是数据结构中的常见操作：把所有元素都访问一遍

线性数据结构的遍历比较简单

正序遍历
逆序遍历

根据节点访问顺序的不同，二叉树的常见遍历方式有4种

前序遍历（Preorder Traversal）
中序遍历（Inorder Traversal）
后序遍历（Postorder Traversal）
层序遍历（Level Order Traversal）

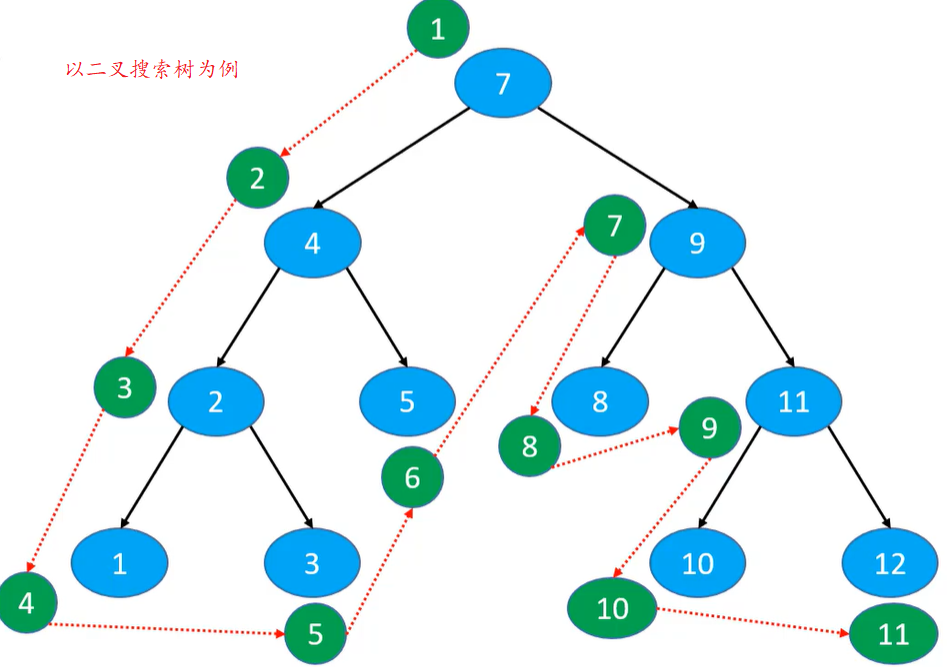
前序遍历（递归/迭代）

访问顺序：根节点、前序遍历左子树、前序遍历右子树

应用：树状结构展示（注意左右子树的顺序）

中序遍历（递归/迭代）

访问顺序：中序遍历左子树、根节点、中序遍历右子树

应用：二叉搜索树的中序遍历按升序或降序处理节点

后序遍历（递归 / 迭代）

访问顺序：后序遍历左子树、后序遍历右子树、根节点

应用：适用于一些先子后父的操作

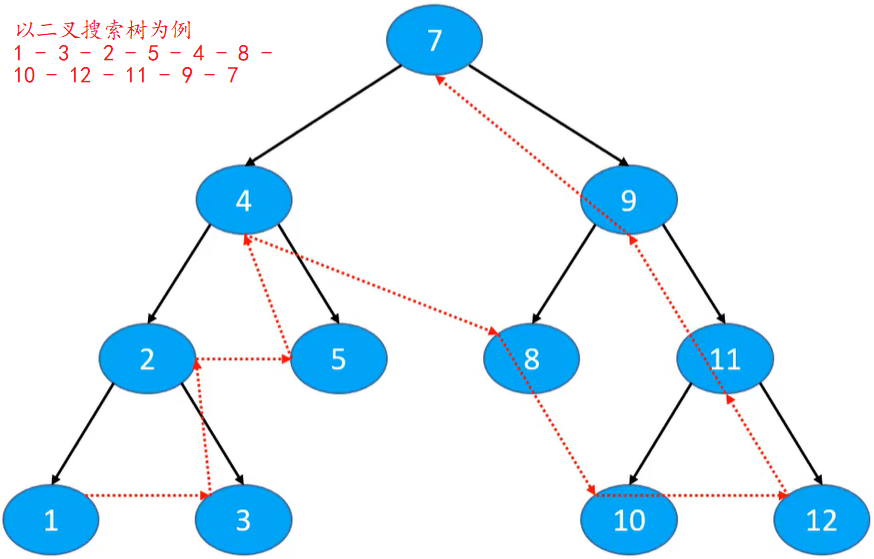
层序遍历 (迭代实现：队列)

//实现思路
// 1. 将根节点入队
// 2. 循环执行以下操作，直到队列为空
//    ① 将队头节点 A 出队，进行访问
//    ② 将 A 的左子节点入队
//    ③ 将 A 的右子节点入队

访问顺序：从上到下、从左到右依次访问每一个节点

应用：① 计算二叉树的高度 ② 判断一棵树是否为完全二叉树

表达式树

四则运算的表达式可以分为3种

前缀表达式（prefix expression），又称为波兰表达式
中缀表达式（infix expression）
后缀表达式（postfix expression），又称为逆波兰表达式

如果将表达式的操作数作为叶子节点，运算符作为父节点（假设只是四则运算）

这些节点刚好可以组成一棵二叉树
比如表达式：A / B + C * D – E

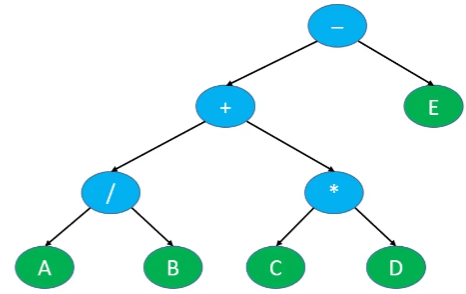
如果对这棵二叉树进行遍历

前序遍历

- + / A B * C D E
刚好就是前缀表达式（波兰表达式）

中序遍历

A / B + C * D – E
刚好就是中缀表达式（波兰表达式）

后序遍历

A B / C D * + E –
刚好就是后缀表达式（逆波兰表达式）

二叉树遍历的应用

前序遍历：树状结构展示(注意左右子树的顺序)
中序遍历：二叉搜索树的中序遍历按升序或者降序处理节点
后序遍历：适用于一些先子后父的操作
层序遍历：①计算二叉树的高度。②判断一棵树是否为完全二叉树

根据遍历结果重构二叉树

前序遍历 + 中序遍历 => 唯一的一颗二叉树
后序遍历 + 中序遍历 => 唯一的一颗二叉树
前序遍历 + 后序遍历 => 如果它是一棵真二叉树，结果是唯一的。否则不然结果不唯一。

###0 前驱节点**(predecessor)**

理解：中序遍历时的前一个节点 “删除节点要使用该知识”

如果是二叉搜索树，前驱节点就是前一个比它小的节点

###1 后继节点**(successor)**

理解：中序遍历时的后一个节点 “删除节点要使用该知识”

如果是二叉搜索树，后继节点就是后一个比它大的节点

###2 打印二叉树的工具

https://github.com/CoderMJLee/BinaryTrees

使用步骤：

实现 BinaryTreeInfo 接口
调用打印API ：BinaryTrees.println(bst);

###3 二叉树遍历非递归实现思路

前序遍历-非递归

利用栈实现(法一)

设置 node = root
循环执行以下操作
- 如果 node != null
  - 对 node 进行访问
  - 将 node.right 入栈
  - 设置 node = node.left
- 如果 node == null
  - 如果栈为空，结束遍历
  - 如果栈不为空，弹出栈顶元素并赋值给 node

利用栈实现(法二)

将 root 入栈
循环执行以下操作，直到栈为空
- 弹出栈顶节点 top，进行访问
- 将 top.right 入栈
- 将 top.left 入栈

中序遍历-非递归

利用栈实现：

设置 node = root
循环执行以下操作
- 如果 node != null
  - 将 node 入栈
  - 设置 node = node.left
- 如果 node == null
  - 如果栈为空，结束遍历
  - 如果栈不为空，弹出栈顶元素并赋值给 node
    - 对 node 进行访问
    - 设置 node = node.right

后序遍历 – 非递归

利用栈实现

将 root 入栈
循环执行以下操作，直到栈为空
- 如果栈顶节点是叶子节点或者上一次访问的节点是栈顶节点的子节点 => 弹出栈顶节点，进行访问
- 否则 => 将栈顶节点的right、left按顺序入栈

###4 二叉树代码实现

/**
 * @Description 二叉树
 * @Author monap
 * @Date 2021/10/10 20:10
 */
@SuppressWarnings("unchecked")
public class BinaryTree<E> implements BinaryTreeInfo {
    protected int size;
    /**
     * 根节点
     */
    protected Node<E> root;

    /**
     * 节点内部类
     */
    protected static class Node<E> {
        E element;
        Node<E> left; // 左子节点
        Node<E> right; // 右子节点
        Node<E> parent; // 父节点

        /**
         * 左右节点可能没有，不必须
         */
        public Node(E element, Node<E> parent) {
            this.element = element;
            this.parent = parent;
        }

        public boolean isLeaf() {
            return left == null && right == null;
        }

        public boolean hasTwoChildren() {
            return left != null && right != null;
        }

        public boolean isLeftChild() {
            return parent != null && this == parent.left;
        }

        public boolean isRightChild() {
            return parent != null && this == parent.right;
        }

        public Node<E> getSibling() {
            if (isLeftChild()) {
                return parent.right;
            }
            if (isRightChild()) {
                return parent.left;
            }
            return null;
        }

        @Override
        public String toString() {
            String parentStr = "null";
            if (parent != null) {
                parentStr = parent.element.toString();
            }
            return element + "_P(" + parentStr + ")";
        }
    }

    protected Node<E> createNode(E element, Node<E> parent) {
        return new Node<>(element, parent);
    }

    /**
     * 元素的数量
     */
    public int size() {
        return size;
    }

    /**
     * 是否为空
     */
    public boolean isEmpty() {
        return size == 0;
    }

    /**
     * 对外接口，用于传出去遍历到的元素(类似于Comparator定制排序)
     */
    public static abstract class Visitor<E> {
        boolean stop;

        // 如果返回true就停止遍历
        public abstract boolean visit(E element);
    }

    /**
     * 前序遍历（非递归方式）、使用栈实现
     */
    public void preorderTraversal(Visitor<E> visitor) {
        if (visitor == null || root == null) return;
        Node<E> node = root;
        Stack<Node<E>> stack = new Stack<>();
        while (true) {
            if (node != null) {
                // 访问node节点
                if (visitor.visit(node.element)) return;
                // 将右子节点入栈
                if (node.right != null) {
                    stack.push(node.right);
                }
                // 向左左
                node = node.left;
            } else if (stack.isEmpty()) {
                return;
            } else {
                // 处理右边
                node = stack.pop();
            }
        }
    }

    /**
     * 前序遍历（递归方式）
     */
    public void preorderTraversal2(Visitor<E> visitor) {
        if (visitor == null) return;
        preorderTraversal(root, visitor);
    }

    protected void preorderTraversal(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) {
            return;
        }
        // System.out.println(node.element);
        // visitor.visit(node.element);//定制
        // if(visitor.stop) return;
        visitor.stop = visitor.visit(node.element);
        preorderTraversal(node.left, visitor);
        preorderTraversal(node.right, visitor);
    }

    /**
     * 中序遍历（非递归方式）、利用栈实现
     */
    public void inorderTraversal(Visitor<E> visitor) {
        if (visitor == null || root == null) return;
        Node<E> node = root;
        Stack<Node<E>> stack = new Stack<>();
        while (true) {
            if (node != null) {
                stack.push(node);
                node = node.left;
            } else if (stack.isEmpty()) {
                return;
            } else {
                node = stack.pop();
                // 访问node节点
                if (visitor.visit(node.element)) return;
                // 让右节点进行中序遍历
                node = node.right;
            }
        }
    }

    /**
     * 中序遍历（递归方式）
     */
    public void inorderTraversal2(Visitor<E> visitor) {
        if (visitor == null) {
            return;
        }
        inorderTraversal(root, visitor);
    }

    protected void inorderTraversal(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) {
            return;
        }
        inorderTraversal(node.left, visitor);
        // visitor.visit(node.element);
        if (visitor.stop) {
            return;
        }
        visitor.stop = visitor.visit(node.element);
        inorderTraversal(node.right, visitor);
    }

    /**
     * 后序遍历（非递归方式）、利用栈实现
     */
    public void postorderTraversal(Visitor<E> visitor) {
        if (visitor == null || root == null) return;
        // 记录上一次弹出访问的节点
        Node<E> prev = null;
        Stack<Node<E>> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            Node<E> top = stack.peek();
            if (top.isLeaf() || (prev != null && prev.parent == top)) {
                prev = stack.pop();
                // 访问node节点
                if (visitor.visit(prev.element)) return;
            } else {
                if (top.right != null) {
                    stack.push(top.right);
                }
                if (top.left != null) {
                    stack.push(top.left);
                }
            }
        }
    }

    /**
     * 后序遍历（递归方式）
     */
    public void postorderTraversal2(Visitor<E> visitor) {
        if (visitor == null) {
            return;
        }
        postorderTraversal(root, visitor);
    }

    protected void postorderTraversal(Node<E> node, Visitor<E> visitor) {
        if (node == null || visitor.stop) {
            // visitor.stop中止递归
            return;
        }
        postorderTraversal(node.left, visitor);
        postorderTraversal(node.right, visitor);
        // visitor.visit(node.element);
        if (visitor.stop) {
            return; // 中止当前打印 ↓
        }
        visitor.stop = visitor.visit(node.element);
    }

    /**
     * 层序遍历（迭代：队列）
     */
    public void levelOrderTraversal(Visitor<E> visitor) {
        if (root == null || visitor == null) {
            return;
        }
        Queue<Node<E>> queue = new LinkedList<>();
        // 将根节点入队
        queue.offer(root);
        while (!queue.isEmpty()) {
            // 将头节点出队
            Node<E> node = queue.poll();
            // System.out.println(node.element);
            // visitor.visit(node.element);
            if (visitor.visit(node.element)) {
                return;
            }
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

    /**
     * 清空所有元素
     */
    public void clear() {
        root = null;
        size = 0;
    }

    //---------------------------

    /**
     * 利用前序遍历进行简单的树状结构展示
     */
    @Override
    public String toString() {
        StringBuilder str = new StringBuilder();
        toString(root, str, "");
        return str.toString();
    }

    protected void toString(Node<E> node, StringBuilder str, String prefix) {
        if (node == null) {
            return;
        }
        str.append(prefix).append(node.element).append("\n");
        toString(node.left, str, prefix + "L-");
        toString(node.right, str, prefix + "R-");
    }

    //---------------------------

    /**
     * 利用中序遍历求某个节点的前驱节点
     */
    protected Node<E> predecessor(Node<E> node) {
        if (node == null) {
            return null;
        }
        // 前驱节点在左子树中：node.left.right.right...
        Node<E> p = node.left;
        if (p != null) {
            while (p.right != null) {
                p = p.right;
            }
            return p;
        }
        // 从祖父节点中寻找前驱节点
        while (node.parent != null && node == node.parent.left) {
            node = node.parent;
        }
        // 情况一：node.parent == null ↓
        // 情况二：node == node.parent.right ↓
        return node.parent;
    }

    /**
     * 利用中序遍历求某个节点的后继节点
     */
    protected Node<E> successor(Node<E> node) {
        if (node == null) {
            return null;
        }
        // 前驱节点在右子树中：node.right.left.left...
        Node<E> p = node.right;
        if (p != null) {
            while (p.left != null) {
                p = p.left;
            }
            return p;
        }
        // 从祖父节点中寻找前驱节点
        while (node.parent != null && node == node.parent.right) {
            node = node.parent;
        }
        // 情况一：node.parent == null ↓
        // 情况二：node == node.parent.left ↓
        return node.parent;
    }

    //---------------------------

    /**
     * 计算二叉树的高度（递归）
     */
    public int heightByRecursion() {
        return height(root);
    }

    /**
     * 获取某一个节点的高度
     */
    protected int height(Node<E> node) {
        if (node == null) {
            return 0;
        }
        return 1 + Math.max(height(node.left), height(node.right));
    }

    /**
     * 利用层序遍历计算二叉树的高度（迭代）
     */
    public int heightByLevelOrderTraversal() {
        if (root == null) {
            return 0;
        }
        int height = 0;
        // 存储着每一层的元素数量
        int levelSize = 0;
        Queue<Node<E>> queue = new LinkedList<>();
        // 将根节点入队
        queue.offer(root);
        while (!queue.isEmpty()) {
            levelSize = queue.size();
            for (int i = 0; i < levelSize; i++) {
                Node<E> node = queue.poll();
                assert node != null;
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            height++;
        }
        return height;
    }

    /**
     * 利用层序遍历判断一颗树是否为完全二叉树
     */
    public boolean isComplete() {
        if (root == null) {
            return false;
        }
        Queue<Node<E>> queue = new LinkedList<>();
        // 将根节点入队
        queue.offer(root);
        boolean leaf = false;
        while (!queue.isEmpty()) {
            // 将头节点出队
            Node<E> node = queue.poll();
            if (leaf && !node.isLeaf()) {
                return false;
            }

            if (node.left != null) {
                queue.offer(node.left);
            } else if (node.right != null) {
                //node.left == null && node.right != null
                return false;
            }

            if (node.right != null) {
                queue.offer(node.right);
            } else {
                //node.right == null
                leaf = true;
            }
        }
        return true;
    }

    /**
     * 使用前序遍历翻转二叉树（所有遍历方式都可实现）
     *
     * @param root
     * @return
     */
    public Node<E> invertTree(Node<E> root) {
        if (root == null) {
            return null;
        }
        Node<E> tmp = root.left;
        root.left = root.right;
        root.right = tmp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }

    //---------------------------

    /**
     * 实现BinaryTreeInfo接口，进行高级的树状结构展示
     */
    @Override
    public Object root() {
        return root;
    }

    @Override
    public Object left(Object node) {
        return ((Node<E>) node).left;
    }

    @Override
    public Object right(Object node) {
        return ((Node<E>) node).right;
    }

    @Override
    public Object string(Object node) {
        return node;
    }
}

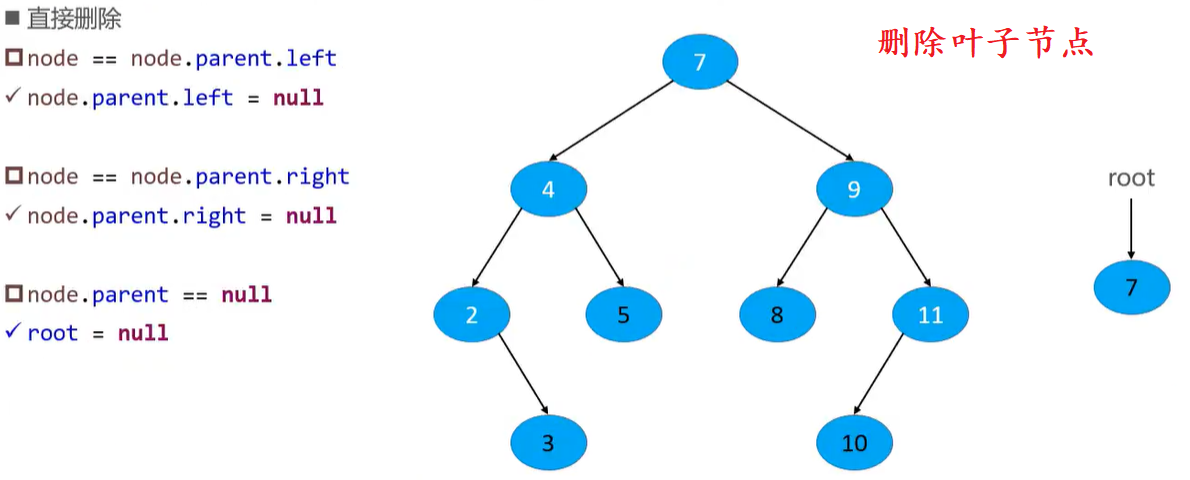
二叉搜索树

引入

在 n 个动态的整数中搜索某个整数？（查看其是否存在）。

假设使用动态数组存放元素，从第 0 个位置开始遍历搜索，平均时间复杂度：O(n)。
- 如果维护一个有序的动态数组，使用二分搜索，最坏时间复杂度：O(logn)。但是添加、删除的平均时间复杂度是 O(n)。

针对这个需求，有没有更好的方案？=> 使用二叉搜索树，添加、删除、搜索的最坏时间复杂度均可优化至：O(logn)级别 <==> O(h) 复杂度只与h有关

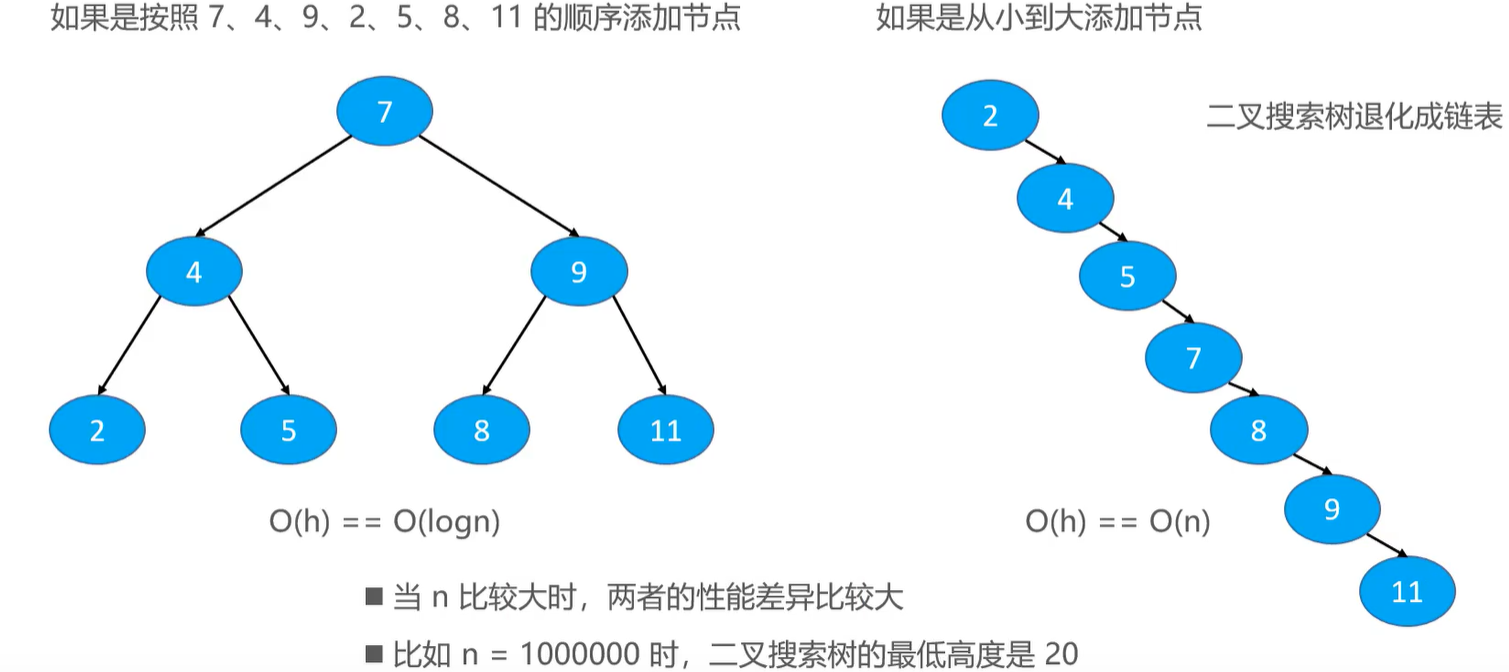
理解

二叉搜索树是二叉树的一种，是应用非常广泛的一种二叉树，英文简称为 BST。

又被称为：二叉查找树、二叉排序树
任意一个节点的值都大于其左子树所有节点的值
任意一个节点的值都小于其右子树所有节点的值
它的左右子树也是一棵二叉搜索树

二叉搜索树可以大大提高搜索数据的效率

二叉搜索树存储的元素必须具备可比较性

比如 int、double 等
如果是自定义类型，需要指定比较方式
不允许为 null

接口设计

由于二叉搜索树继承于二叉树，只需要实现添加，删除，包含的接口

注意：对于当前使用的二叉树来说，它的元素没有索引的概念。

图解

添加节点

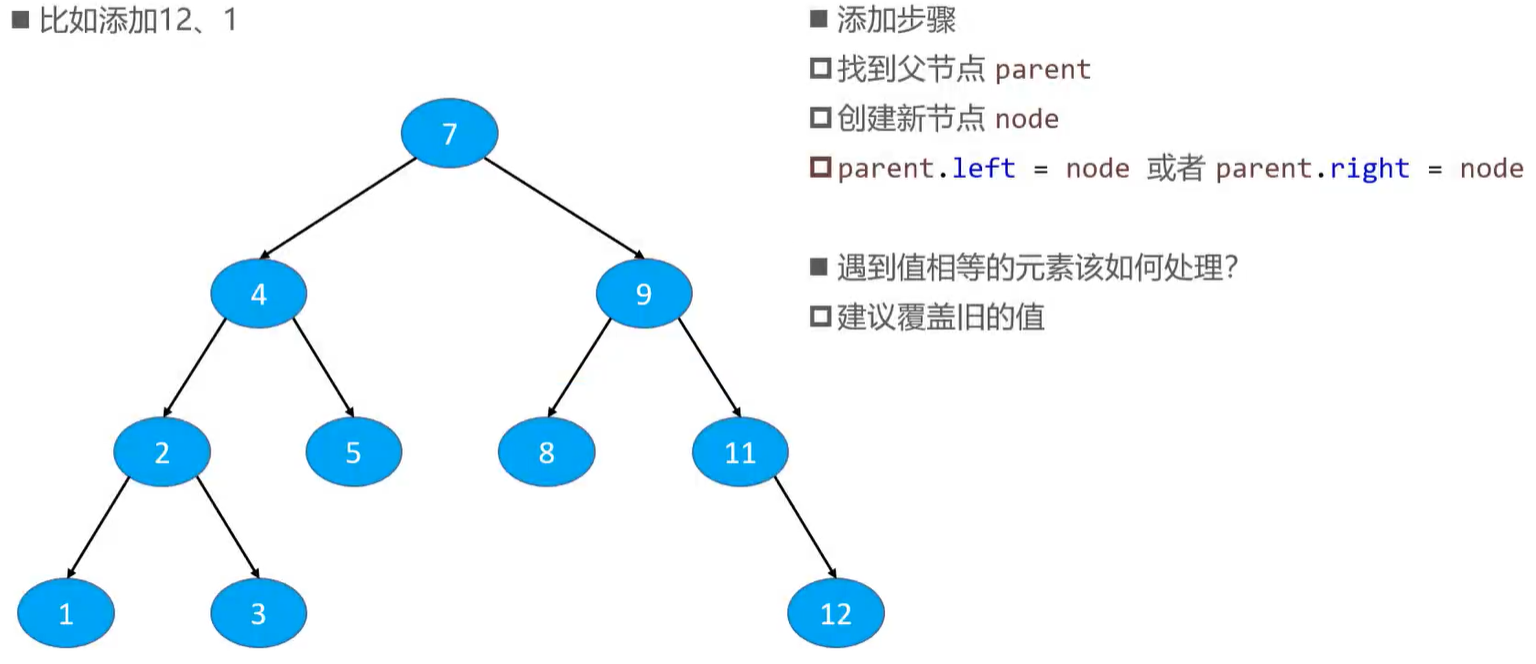
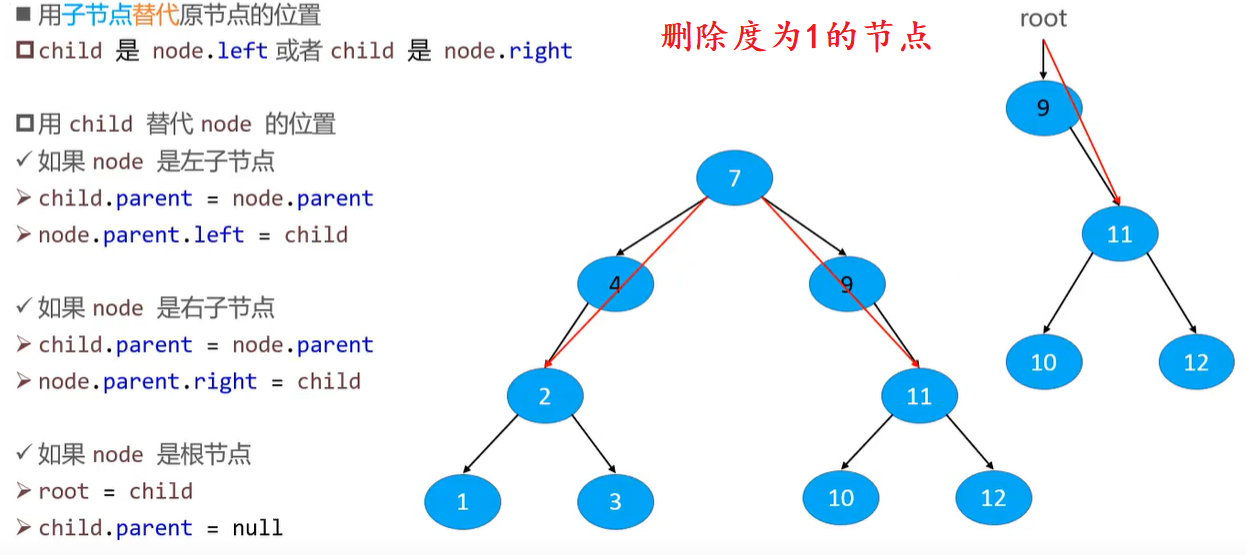
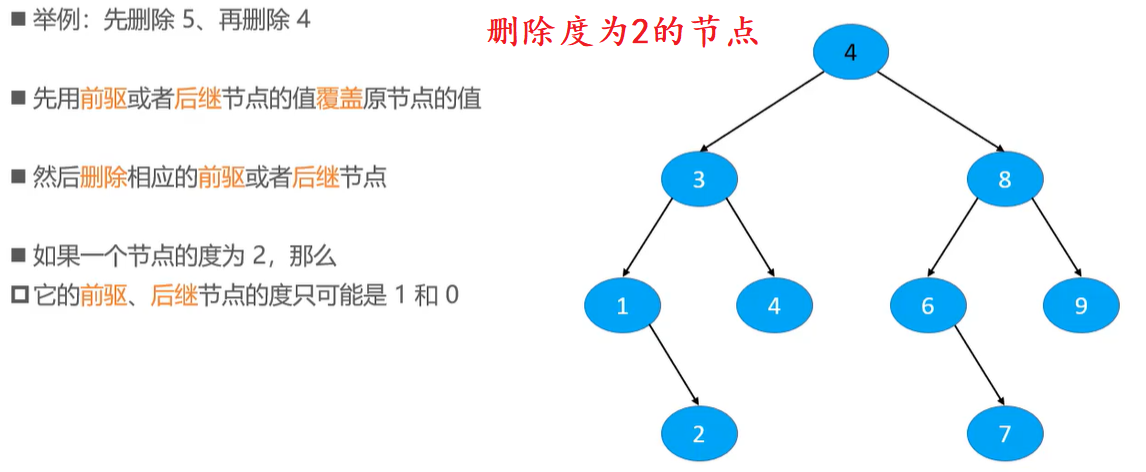
删除节点

代码实现

/**
 * @Description 二叉搜索树
 * @Author monap
 * @Date 2021/10/10 20:17
 */
@SuppressWarnings("unchecked")
public class BSTree<E> extends BinaryTree<E> {
    /**
     * 比较器定制排序
     */
    protected Comparator<E> comparator;

    public BSTree() {
        this(null);
    }

    public BSTree(Comparator<E> comparator) {
        this.comparator = comparator;
    }

    /**
     * 检查添加元素是否为空
     */
    protected void elementNoNullCheck(E element) {
        if (element == null) {
            throw new IllegalArgumentException("element must no be null!");
        }
    }

    /**
     * 比较元素大小，返回值为0代表e1等于e2，大于0代表e1大于e2，小于0代表e1小于e2
     */
    protected int compare(E e1, E e2) {
        if (comparator != null) {
            return comparator.compare(e1, e2);
        }
        // 注意：不在上面写死（BinarySearchTree<E extends Comparable>），
        // 而是在这里进行强制转换,如果E没有实现此接口就会报错提醒。否则
        // 如果E没有实现此接口在编译时就会报错，我们希望两种比较方式都可以使用。
        return ((Comparable<E>) e1).compareTo(e2);
    }

    /**
     * 添加元素
     */
    public void add(E element) {
        elementNoNullCheck(element);
        // 添加第一个节点（根节点）
        if (root == null) {
            root = createNode(element, null);
            size++;
            // 新添加节点之后的处理
            afterAdd(root);
            return;
        }
        // 如果添加的不是第一个节点：
        // 1.找到待添加位置的父节点
        Node<E> parent = root;
        Node<E> node = root;
        int cmp = 0;
        while (node != null) {
            cmp = compare(element, node.element);
            parent = node;
            if (cmp > 0) {
                node = node.right;
            } else if (cmp < 0) {
                node = node.left;
            } else {
                // 一般覆盖（不同对象可能有相同的比较参数）
                node.element = element;
                return;
            }
        }
        // 2.判断插入父节点的左子节点还是右子节点
        Node<E> newNode = createNode(element, parent);
        if (cmp > 0) {
            parent.right = newNode;
        } else {
            parent.left = newNode;
        }
        size++;
        // 新添加节点之后的处理
        afterAdd(newNode);
    }

    /**
     * 添加node节点后所需要做的调整（二叉搜索树不需要调整）
     */
    protected void afterAdd(Node<E> node) {
    }

    /**
     * 删除元素
     */
    public void remove(E element) {
        remove(node(element));
    }

    /**
     * 根据元素找到对应节点
     */
    protected Node<E> node(E element) {
        Node<E> node = root;
        while (node != null) {
            int cmp = compare(element, node.element);
            if (cmp == 0) {
                return node;
            }
            if (cmp > 0) {
                node = node.right;
            } else {
                node = node.left;
            }
        }
        return null;
    }

    /**
     * 删除对应节点
     */
    protected void remove(Node<E> node) {
        if (node == null) {
            return;
        }
        size--;
        // 考虑度为2的节点，转化为度为1
        if (node.hasTwoChildren()) {
            // 后继节点
            Node<E> s = successor(node);
            // 用后继节点的值覆盖度为2的节点的值
            node.element = s.element;
            // 删除后继节点
            node = s;
        }
        // 删除node节点（能到这则说明node的度必为0或1）
        Node<E> replacement = node.left != null ? node.left : node.right;
        // node是度为1的节点
        if (replacement != null) {
            //更改parent
            replacement.parent = node.parent;
            // 更改parent的left，right指向
            // node是度为1的节点也是根节点
            if (node.parent == null) {
                root = replacement;
            } else if (node == node.parent.left) {
                node.parent.left = replacement;
            } else {
                // 在右边
                node.parent.right = replacement;
            }
            // 此时开始恢复平衡(AVL树 或 RB树需要实现此方法)
            afterRemove(node, replacement);
        } else if (node.parent == null) {
            // node是叶子节点也是根节点
            root = null;
            afterRemove(node, null);
        } else {
            // node是叶子节点但不是根节点
            if (node == node.parent.left) {
                node.parent.left = null;
            } else {
                node.parent.right = null;
            }
            // 此时开始恢复平衡(AVL树 或RB树 需要实现此方法)
            afterRemove(node, null);
        }
    }

    /**
     * 删除node节点后所需要做的调整（二叉搜索树不需要调整）
     */
    protected void afterRemove(Node<E> node, Node<E> replacement) {
    }

    /**
     * 是否包含某元素
     */
    public boolean contains(E element) {
        return node(element) != null;
    }
}

测试

public class BSTreeTest {
	@Test
	public void test() {
		//测试二叉树打印工具
		//  ┌─_A_─┐
		//  │     │
		// _B_   _C_
		BinaryTrees.println(new BinaryTreeInfo() {
			@Override
			public Object string(Object node) {
				return "_" + node.toString() + "_";
			}
			
			@Override
			public Object root() {
				return "A";
			}
			
			@Override
			public Object right(Object node) {
				if(node.equals("A")) return "C";
				return null;
			}
			
			@Override
			public Object left(Object node) {
				if(node.equals("A")) return "B";
				return null;
			}
		});
	}
	
	@Test
	public void test1() {
		// 自然排序
		Integer[] data = new Integer[] { 7, 4, 9, 2, 5, 8, 11, 3, 12, 1 };
		BSTree<Integer> bst = new BSTree<>();
		for (int i = 0; i < data.length; i++) {
			bst.add(data[i]);
		}
		BinaryTrees.println(bst, PrintStyle.INORDER);
		String str = BinaryTrees.printString(bst);
		Files.writeToFile("D:/1.txt", str);
	}

	@Test
	public void test2() {
		// 定制排序
		Integer[] data = new Integer[] { 7, 4, 9, 2, 5, 8, 11, 3, 12, 1 };
		BSTree<Person> bst = new BSTree<>(new Comparator<Person>() {
			@Override
			public int compare(Person e1, Person e2) {
				return e2.getAge() - e1.getAge();
			}
		});
		for (int i = 0; i < data.length; i++) {
			bst.add(new Person(data[i]));
		}
		BinaryTrees.println(bst);
	}
	
	@Test
	public void test3() {
		//遍历测试
		Integer[] data = new Integer[] { 7, 4, 2, 1, 3, 5, 9, 8, 11, 10, 12};
		BSTree<Integer> bst = new BSTree<>();
		for (int i = 0; i < data.length; i++) {
			bst.add(data[i]);
		}
		BinaryTrees.println(bst);
		BinaryTrees.println(bst);
		//测试前序遍历（递归）
		System.out.println("前序遍历：");
		bst.preorderTraversal(new Visitor<Integer>() {
			public boolean visit(Integer element) {
				System.out.print(element + " ");
				return element == 2 ? true : false;//遍历到值为2停止
			}
		});
		System.out.println();
		//测试中序遍历（递归）
		System.out.println("中序遍历：");
		bst.inorderTraversal(new Visitor<Integer>() {
			public boolean visit(Integer element) {
				System.out.print(element + " ");
				return element == 4 ? true : false;//遍历到值为4停止
			}
		});
		System.out.println();
		//测试后序遍历（递归）
		System.out.println("后序遍历：");
		bst.postorderTraversal(new Visitor<Integer>() {
			public boolean visit(Integer element) {
				System.out.print(element + " ");
				return element == 4 ? true : false;//遍历到值为4停止
			}
		});
		System.out.println();
		//测试层序序遍历（队列）
		System.out.println("层序遍历：");
		bst.levelOrderTraversal(new Visitor<Integer>() {
			public boolean visit(Integer element) {
				System.out.print(element + "_ ");
				return false;//遍历所有
			}
		});
	}
	
	@Test
	public void test4() {
		//遍历的应用测试
		Integer[] data = new Integer[] { 7, 4, 9, 5, 2};
		BSTree<Integer> bst = new BSTree<>();
		for (int i = 0; i < data.length; i++) {
			bst.add(data[i]);
		}
		BinaryTrees.println(bst);
		//1.前序遍历的应用：展示树状结构(其他遍历方式也可以展示树状结构)
		System.out.println(bst);
		//2.层序遍历的应用：计算二叉树的高度
		System.out.println("二叉树高度为：" + bst.height1());//递归方式
		System.out.println("二叉树高度为：" + bst.height2());//层序递归方式
		//3.层序遍历的应用：判断一颗树是否是完全二叉树
		System.out.println("当前二叉搜索树是否为完全二叉树：" + bst.isComplete());
		Integer[] data1 = new Integer[] { 7, 4, 9, 2, 1};
		BSTree<Integer> bst1 = new BSTree<>();
		for (int i = 0; i < data1.length; i++) {
			bst1.add(data1[i]);
		}
		BinaryTrees.println(bst1);
		System.out.println("当前二叉搜索树是否为完全二叉树：" + bst1.isComplete());
	}
	
	@Test
	public void test5() {
		//测试删除
		Integer[] data = new Integer[] { 7, 4, 9, 2, 5, 8, 11, 3, 12, 1 };
		BSTree<Integer> bst = new BSTree<>();
		for (int i = 0; i < data.length; i++) {
			bst.add(data[i]);
		}
		BinaryTrees.println(bst);
		bst.remove(7);
		BinaryTrees.println(bst);
	}
}

class Person implements Comparable<Person> {
	private int age;

	public Person() {
		
	}

	public Person(int age) {
		this.age = age;
	}

	public int getAge() {
		return age;
	}

	public void setAge(int age) {
		this.age = age;
	}

	@Override
	public int compareTo(Person e) {
		return age - e.age;
	}

	@Override
	public String toString() {
		return "age=" + age;
	}
}

public class BSTreeTest {
    @Test
    public void comparatorTest() {
        BSTree<Person> personBSTree = getPersonBSTree();
        BinaryTrees.println(personBSTree, BinaryTrees.PrintStyle.INORDER);
        BinaryTrees.println(personBSTree, BinaryTrees.PrintStyle.LEVEL_ORDER);
    }

    @Test
    public void traversalTest() {
        BSTree<Person> personBSTree = getPersonBSTree();
        BinaryTrees.println(personBSTree, BinaryTrees.PrintStyle.LEVEL_ORDER);
        personBSTree.preorderTraversal(new BinaryTree.Visitor<Person>() {
            @Override
            public boolean visit(Person element) {
//                element.setHeight(element.getHeight() + 1);
                System.out.println(element.getHeight());
                if (element.getHeight() == 2.05) {
                    return true;
                }
                return false;
            }
        });
    }

    @Test
    public void preorderTraversalPrintTest() {
        BSTree<Person> personBSTree = getPersonBSTree();
        System.out.println(personBSTree.toString());
    }

    private BSTree<Person> getPersonBSTree() {
        BSTree<Person> personBSTree = new BSTree<>(new Comparator<Person>() {
            @Override
            public int compare(Person o1, Person o2) {
                return o1.getAge().compareTo(o2.getAge());
            }
        });
        personBSTree.add(new Person("张三",20,1.85));
        personBSTree.add(new Person("李四",16,2.05));
        personBSTree.add(new Person("王二",77,1.54));
        personBSTree.add(new Person("莫言",64,1.99));
        return personBSTree;
    }

    private class Person {
        private String name;
        private Integer age;
        private Double height;

        public Person() {

        }

        public Person(String name, Integer age, Double height) {
            this.name = name;
            this.age = age;
            this.height = height;
        }

        public String getName() {
            return name;
        }

        public void setName(String name) {
            this.name = name;
        }

        public Integer getAge() {
            return age;
        }

        public void setAge(Integer age) {
            this.age = age;
        }

        public Double getHeight() {
            return height;
        }

        public void setHeight(Double height) {
            this.height = height;
        }

        @Override
        public String toString() {
            return age.toString();
        }
    }
}

AVL树

理解

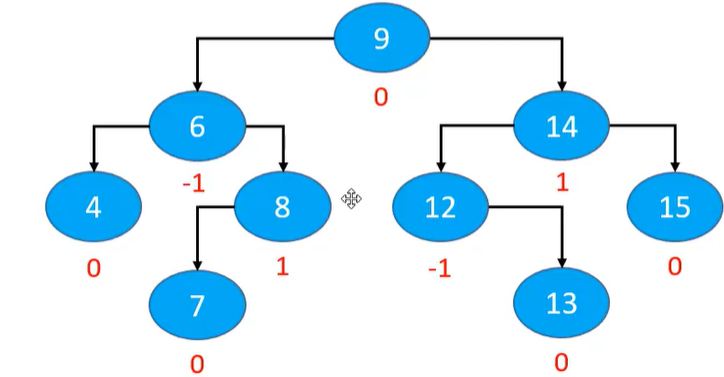
平衡因子（Balance Factor）：某结点的左右子树的高度差(左 - 右)

AVL树的特点:

每个节点的平衡因子只可能是 1、0、-1（绝对值 ≤ 1，如果超过 1，称之为“失衡”）
每个节点的左右子树高度差不超过 1
搜索、添加、删除的时间复杂度是 O(logn)

说明：红黑树的添加删除后的旋转恢复平衡都是O(1)级别的。AVL树添加后的旋转恢复平衡是O(1)级别的，而删除后的旋转恢复平衡操作的最坏情况达到了O(logn)级别

注意：
① AVL树是最早发明的自平衡二叉搜索树之一
② AVL 取名于两位发明者的名字：G. M. Adelson-Velsky 和 E. M. Landis（来自苏联的科学家）

继承机构

添加导致的失衡

示例：往下面这棵子树中添加 13

最坏情况：可能会导致所有祖先节点都失衡
父节点、非祖先节点，都不可能失衡

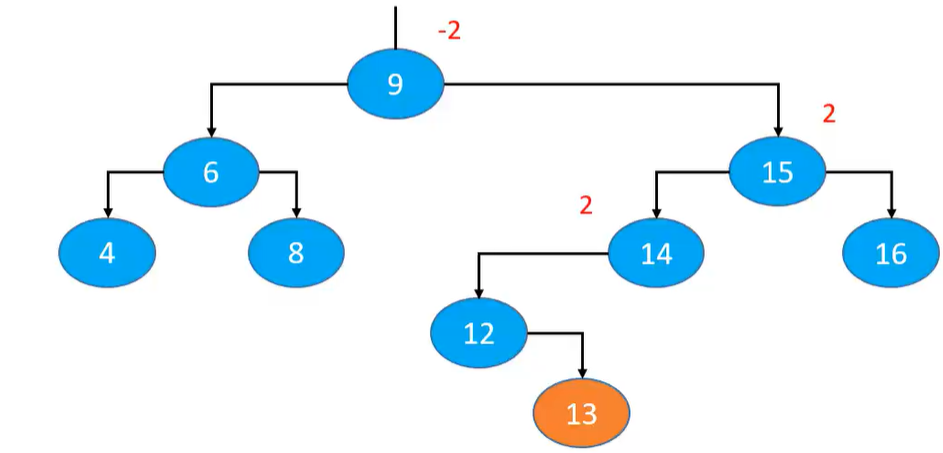
四种添加失衡情况及其处理（有且仅有四种）

LL-g右旋转（单旋）

RR-g左旋转（单旋）

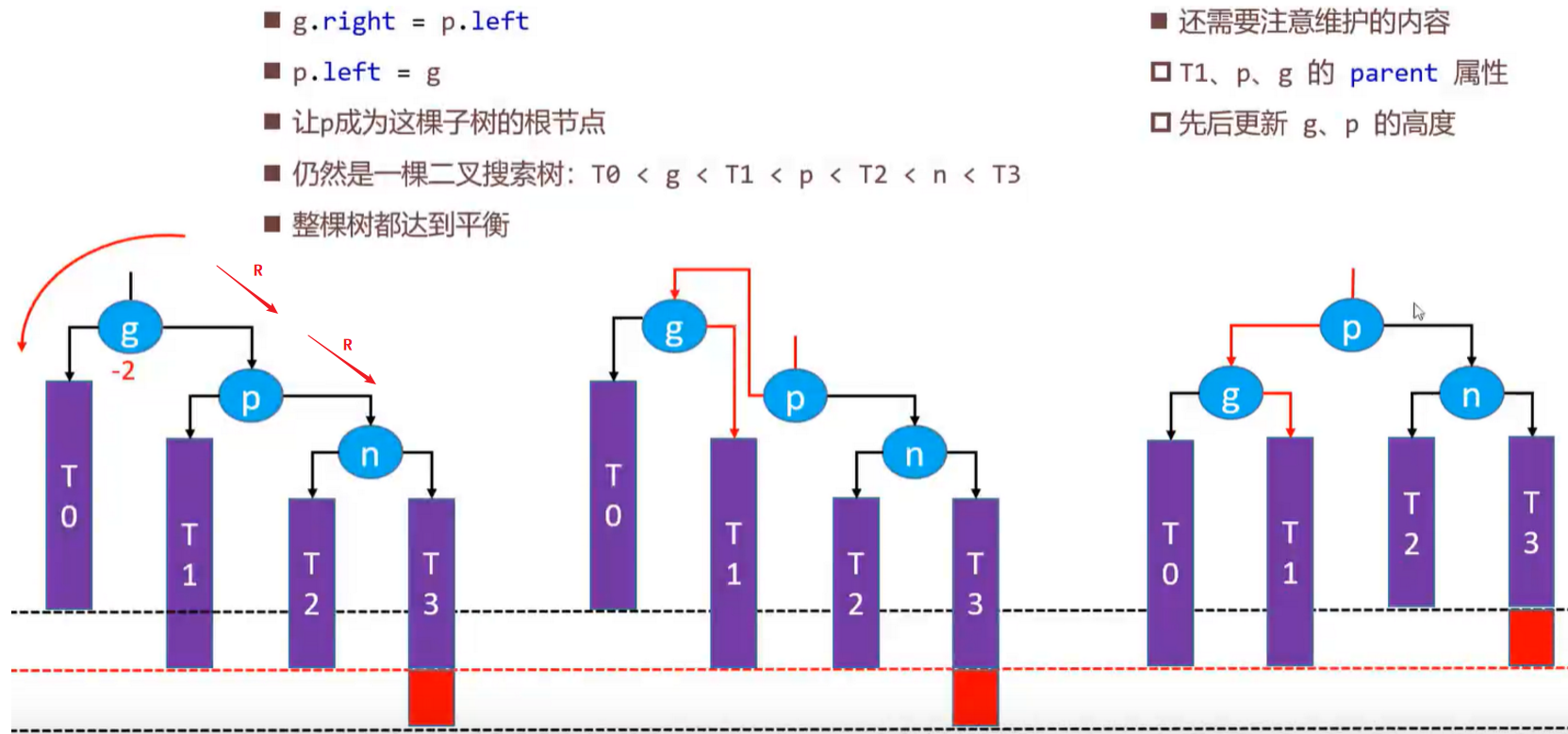
LR-p左旋转，g右旋转(双旋)

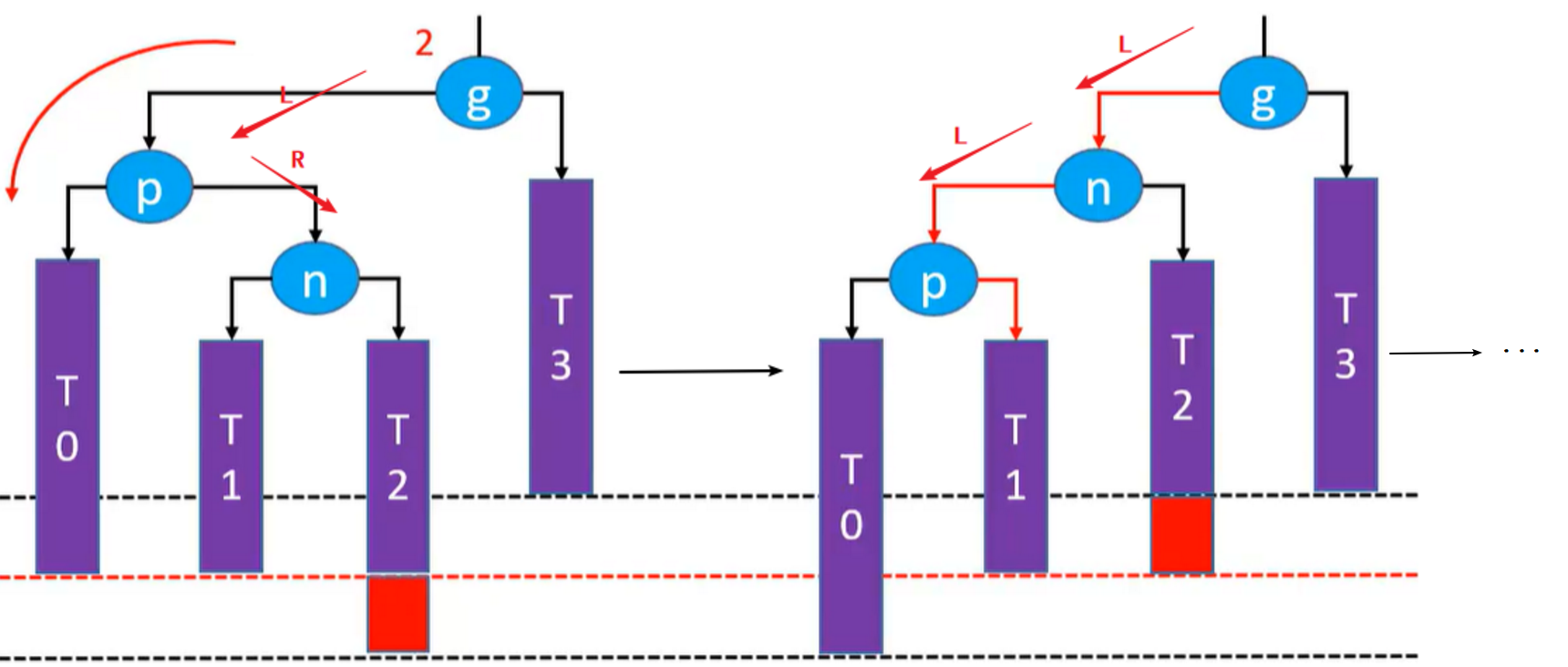
RL-p右旋转，g左旋转(双旋）

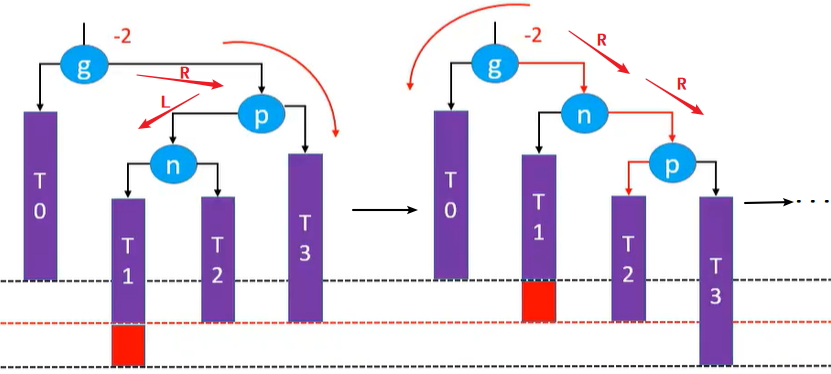
四种添加失衡情况的统一处理

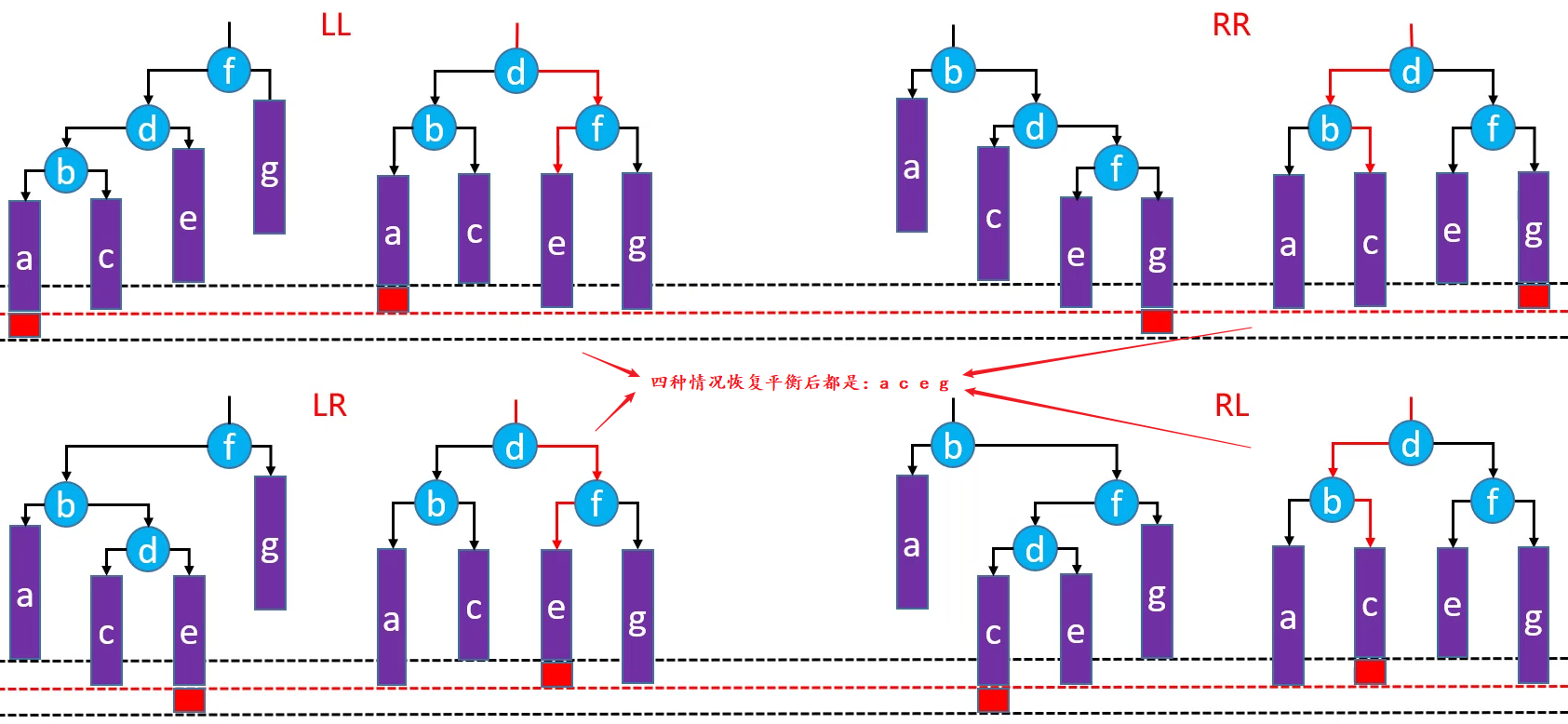
删除导致的失衡

示例：删除下面这棵树的16

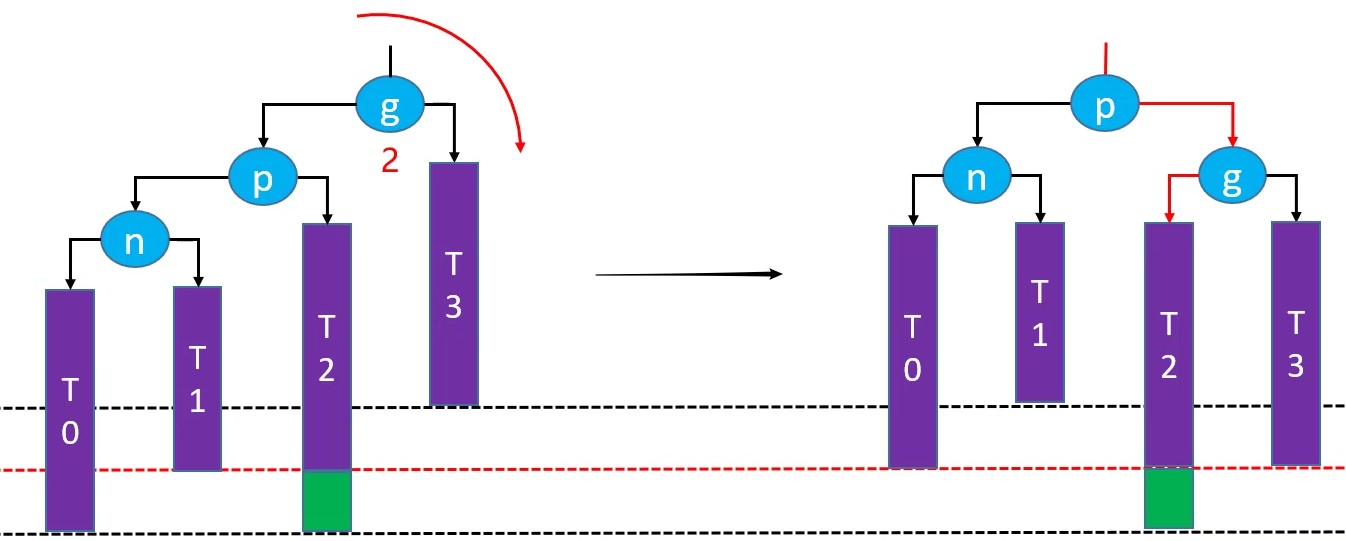
删除后需要使用 LL-右旋转解决失衡的情况

如果绿色节点不存在，更高层的祖先节点可能也会失衡，需要再次恢复平衡，然后又可能导致更高层的祖先节点失衡...
极端情况下，所有祖先节点都需要进行恢复平衡的操作，共 O(logn) 次调整

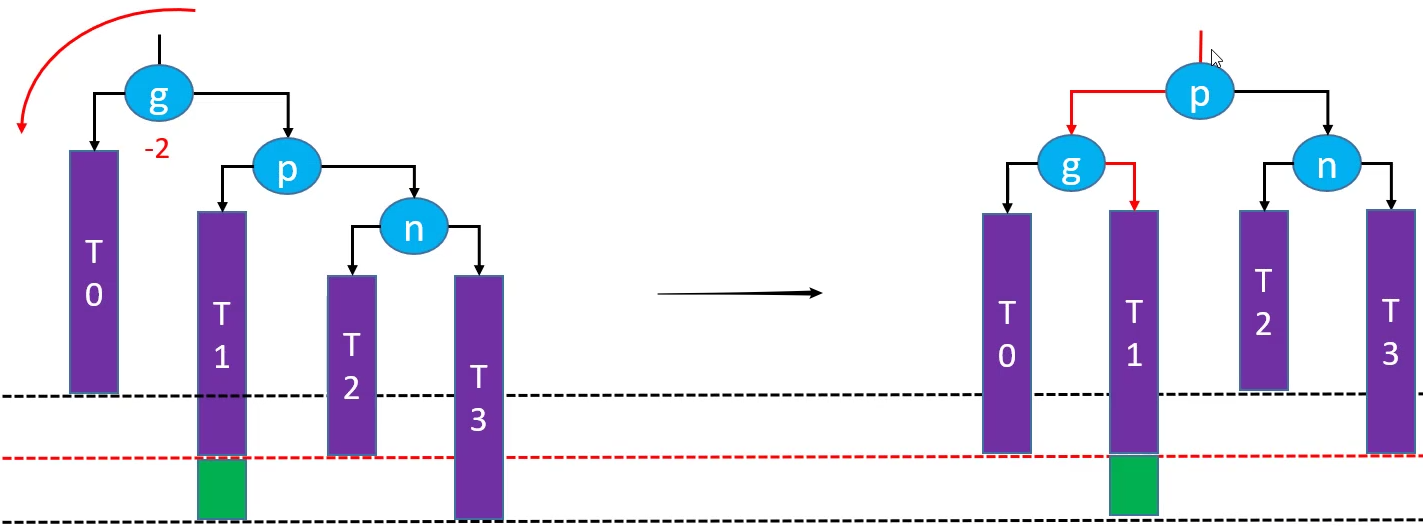
删除后需要使用 RR-左旋转解决失衡的情况

删除后需要使用 LR-p左旋转，g右旋转(双旋) 解决失衡的情况

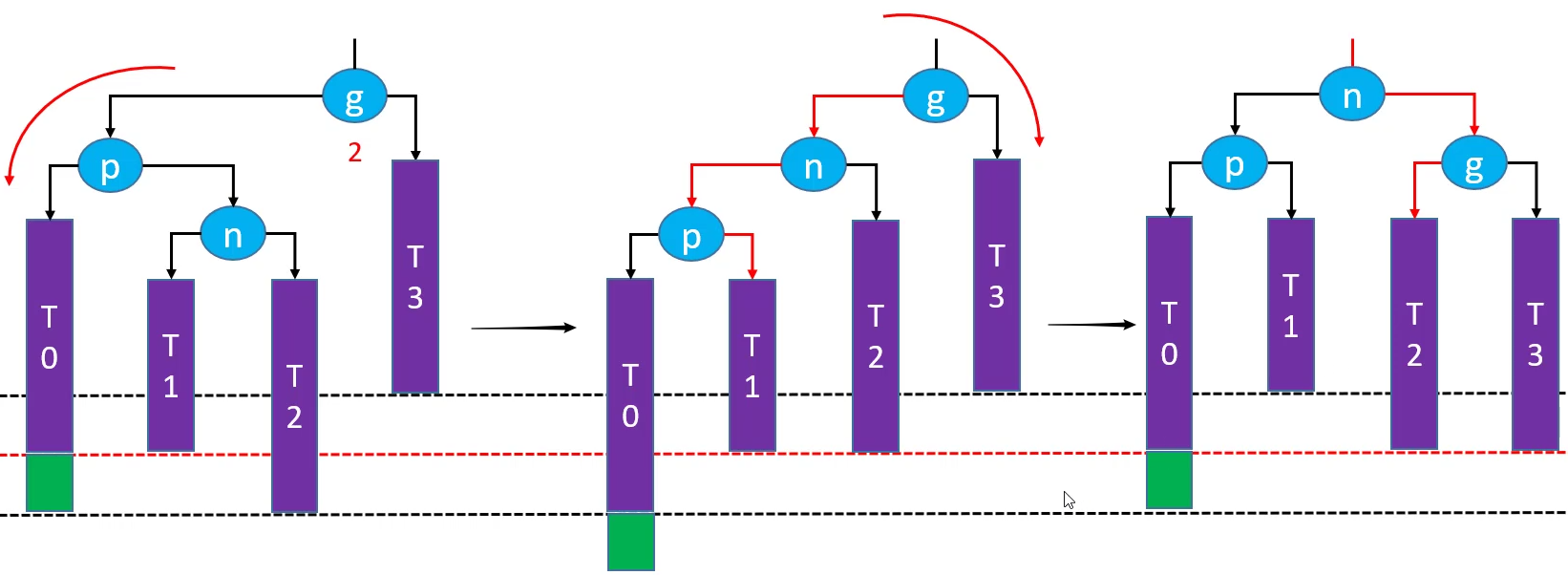
删除后需要使用 RL-p右旋转，g左旋转(双旋）解决失衡的情况

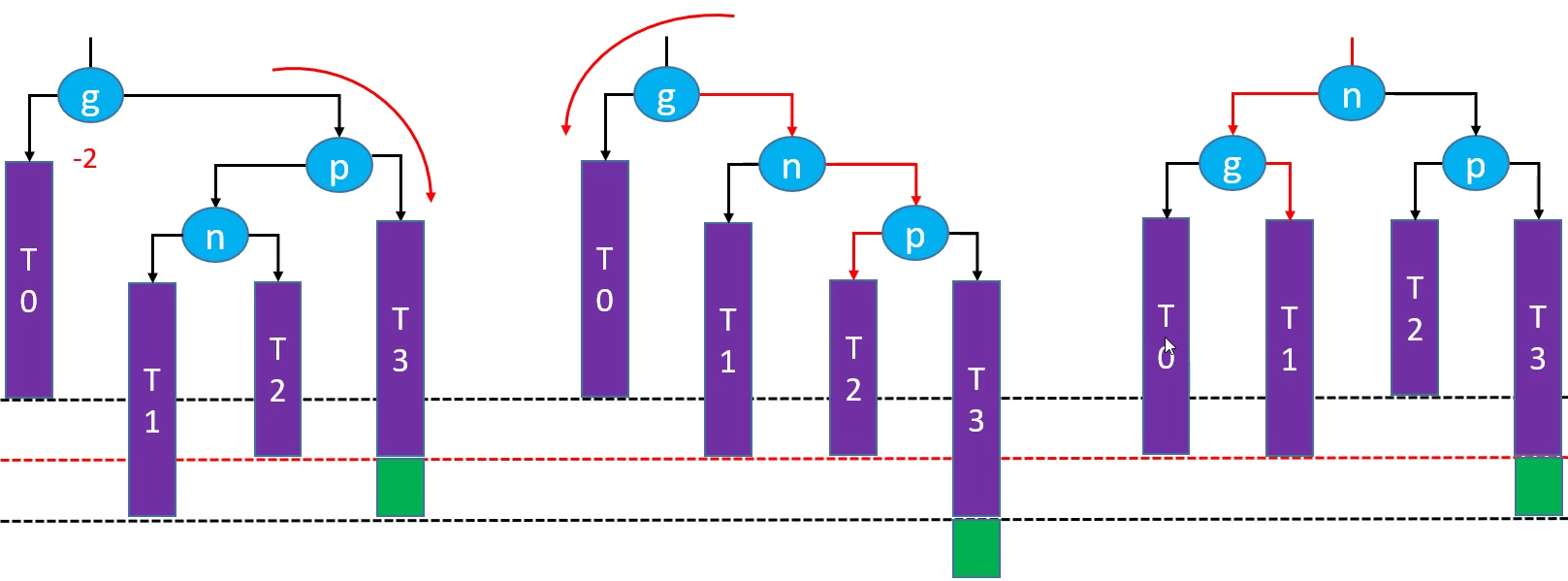
总结

添加

可能会导致 所有祖先节点 都失衡
只要让高度最低的失衡节点恢复平衡，整棵树就恢复平衡【仅需 O(1) 次调整】

删除

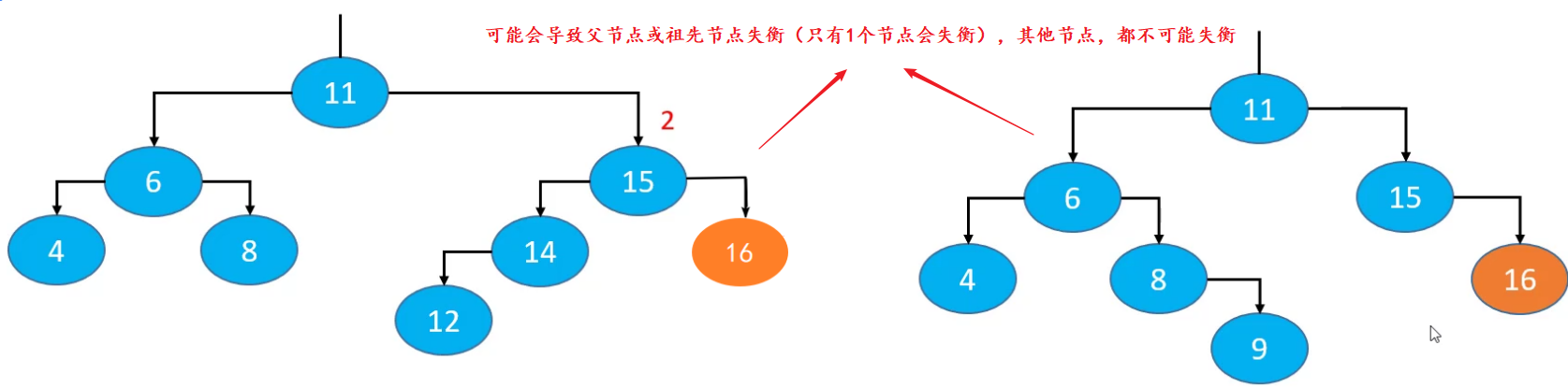
可能会导致父节点或祖先节点失衡（只有1个节点会失衡）
恢复平衡后，可能会导致更高层的祖先节点失衡【最多需要 O(logn) 次调整】

平均时间复杂度

搜索：O(logn)
添加：O(logn)，仅需 O(1) 次的旋转操作
删除：O(logn)，最多需要 O(logn) 次的旋转操作

代码实现

平衡二叉搜索树

/**
 * @Description 平衡二叉搜索树
 * @author Polaris
 * @version
 * @date 2020年3月10日下午8:33:51
 */
public class BBSTree<E> extends BSTree<E>{
	
	public BBSTree() {
		this(null);
	}

	public BBSTree(Comparator<E> comparator) {
		super(comparator);
	}
	
	/**
	 *	左旋转，以RR为例
	 */
	protected void rotateLeft(Node<E> grand) {
		Node<E> parent = grand.right;
		Node<E> child = parent.left;//child就是T1子树
		grand.right = child;
		parent.left = grand;
		
		afterRotate(grand, parent, child);
	}
	
	/**
	 *	右旋转，以LL为例
	 */
	protected void rotateRight(Node<E> grand) {
		Node<E> parent = grand.left;
		Node<E> child = parent.right;
		grand.left = child;
		parent.right = grand;
		
		afterRotate(grand, parent, child);
	}
	
	/**
	 * 	抽取左旋转和右旋转中的重复代码
	 */
	protected void afterRotate(Node<E> grand,Node<E> parent,Node<E> child) {
		//更新parent的parent（让parent成为子树的根节点）
		parent.parent = grand.parent;
		if(grand.isLeftChild()) {
			grand.parent.left = parent;
		} else if(grand.isRightChild()) {
			grand.parent.right = parent;
		} else { //grand是root节点
			root = parent;
		}
		//更新child的parent
		if(child != null) {
			child.parent = grand;		
		}
		//更新grand的parent
		grand.parent = parent;
	}
	
	/**
	 * 	统一旋转
	 */
	protected void rotate(
			Node<E> r, //之前的根节点
			Node<E> a,Node<E> b,Node<E> c,
			Node<E> d,
			Node<E> e,Node<E> f,Node<E> g) {
		//让d成为这棵子树的根节点
		d.parent = r.parent;
		if(r.isLeftChild()) {
			r.parent.left = d;
		} else if(r.isRightChild()) {
			r.parent.right = d;
		} else {
			root = d;
		}
		//处理a,b,c之间的关系
		b.left = a;
		if(a != null) {
			a.parent = b;
		}
		b.right = c;
		if(c != null) {
			c.parent = b;
		}
		
		//处理e,f,g之间的关系
		f.left = e;
		if(e != null) {
			e.parent = f;
		}
		f.right = g;
		if(g != null) {
			g.parent = f;
		}
		
		//处理b,d,f之间的关系
		d.left = b;
		d.right = f;
		b.parent = d;
		f.parent = d;
	}
	
}

AVL树

/**
 * @Description AVL树
 * @author Polaris
 * @version
 * @date 2020年3月10日下午8:35:05
 */
public class AVLTree<E> extends BBSTree<E> {
	
	public AVLTree() {
		this(null);
	}

	public AVLTree(Comparator<E> comparator) {
		super(comparator);
	}
	
	/**
	 * AVL树特有的节点，多了height属性用于计算平衡因子
	 */
	private static class AVLNode<E> extends Node<E> {
		//每个新添加的未经过处理的节点必然是叶子节点（高度默认为 1）
		int height = 1;//AVL树平衡因子：左子树高度 - 右子树高度（默认为叶子节点的高度1）
		
		public AVLNode(E element, Node<E> parent) {
			super(element, parent);
		}
		
		/*
		 * 	更新当前节点自己的高度
		 */
		public void updateHeight() {
			int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
			int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
			height = 1 + Math.max(leftHeight, rightHeight);
		}
		
		/*
		 * 	获取当前节点的平衡因子
		 */
		public int balanceFactor() {
			int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
			int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
			return leftHeight - rightHeight;
		}
		
		/*
		 * 	获取当前节点高度更高一点的子树
		 */
		public Node<E> tallerChild() {
			int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
			int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
			if(leftHeight > rightHeight) return left;
			if(leftHeight < rightHeight) return right;
			//当左右子树相等时，就返回和当前节点同方向(比如当前节点parent的左子树)的子树
			return isLeftChild() ? left :right;
		}
		
		@Override
		public String toString() {
			String parentString = "null";
			if (parent != null) {
				parentString = parent.element.toString();
			}
			return element + "_p(" + parentString + ")_h(" + height + ")";
		}
	}
	
	/**
	 * 	重写createNode，用于创建AVL特有的AVL节点
	 */
	@Override
	protected Node<E> createNode(E element, Node<E> parent) {
		return new AVLNode<>(element, parent);
	}
	
	/**
	 * 	实现添加新节点后的处理操作(通过当前节点找到失衡节点进行调整)
	 */
	@Override
	protected void afterAdd(Node<E> node) {
		while ((node = node.parent) != null) {
			if (isBalanced(node)) {	//如果平衡
				//更新高度（如果采用递归更新高度效率太差，直接在找parent失衡节点时就更新高度）
				updateHeight(node);
			} else {	//如果不平衡(记得要在恢复平衡时更新高度)
				// 恢复平衡
				rebalance(node);
				break;//找到一个不平衡节点恢复平衡则整棵树都平衡
			}
		}
	}
	
	@Override
	protected void afterRemove(Node<E> node,Node<E> replacement) {
		while ((node = node.parent) != null) {
			if (isBalanced(node)) {	//如果平衡
				//更新高度（如果采用递归更新高度效率太差，直接在找parent失衡节点时就更新高度）
				updateHeight(node);
			} else {	//如果不平衡(记得要在恢复平衡时更新高度)
				// 恢复平衡
				rebalance(node);
			}
		}
	}
	
	/**
	 * 	判断当前节点是否平衡
	 */
	private boolean isBalanced(Node<E> node) {
		return Math.abs(((AVLNode<E>)node).balanceFactor()) <= 1;
	}
	
	/**
	 * 	更新某个节点的高度(将强制转换封装为方法)
	 */
	private	void updateHeight(Node<E> node) {
		((AVLNode<E>)node).updateHeight();
	}
	
	//————————方式一：分开处理——————————
	/**
	 * 	恢复平衡（四种失衡情况单独处理）
	 * @param node 高度最低的那个不平衡节点
	 */
	private void rebalance(Node<E> grand) {
		//p是g左右子树中高度较高的子树
		Node<E> parent = ((AVLNode<E>)grand).tallerChild();
		//n是p左右子树中高度较高的子树
		Node<E> node = ((AVLNode<E>)parent).tallerChild();
		if(parent.isLeftChild()) { //L
			if(node.isLeftChild()) { //LL
				rotateRight(grand);//g左旋转
			} else { //LR
				rotateLeft(parent);//p左旋转
				rotateRight(grand);//g右旋转
			}
		} else { //R
			if(node.isLeftChild()) { //RL
				rotateRight(parent);//p右旋转
				rotateLeft(grand);//g左旋转
			} else { //RR
				rotateLeft(grand);
			}
		}
	}
	
	@Override
	protected void afterRotate(Node<E> grand, Node<E> parent, Node<E> child) {
		super.afterRotate(grand, parent, child);
		//更新高度
		updateHeight(grand);//g比较矮
		updateHeight(parent);//p比较高
	}
	
	//————————方式二：统一处理————————
	/**
	 * 	恢复平衡（四种失衡情况一起处理）
	 * @param node 高度最低的那个不平衡节点
	 */
	private void rebalance2(Node<E> grand) {
		//p是g左右子树中高度较高的子树
		Node<E> parent = ((AVLNode<E>)grand).tallerChild();
		//n是p左右子树中高度较高的子树
		Node<E> node = ((AVLNode<E>)parent).tallerChild();
		if(parent.isLeftChild()) { //L
			if(node.isLeftChild()) { //LL
				rotate(grand,node.left,node,node.right, 
						parent,parent.right,grand,grand.right);
			} else { //LR
				rotate(grand,parent.left,parent,node.left,
						node,node.right,grand,grand.right);
			}
		} else { //R
			if(node.isLeftChild()) { //RL
				rotate(grand,grand.left,grand,node.left,
						node,node.right,parent,parent.right);
			} else { //RR
				rotate(grand,grand.left,grand,parent.left,
						parent,node.left,node,node.right);
			}
		}
	}
	
	@Override
	protected void rotate(Node<E> r, Node<E> a, Node<E> b, Node<E> c, Node<E> d, Node<E> e, Node<E> f, Node<E> g) {
		super.rotate(r, a, b, c, d, e, f, g);
		//更新高度
		updateHeight(b);
		updateHeight(f);
		updateHeight(d);
	}
}

测试

public class AVLTreeTest {
	//添加删除测试
	@Test
	public void test() {
		Integer[] data = new Integer[] {
				67,52,92,96,53,95,13,63,34,82,76,54,9,68,39};
		AVLTree<Integer> avl = new AVLTree<>();
		for (int i = 0; i < data.length; i++) {
			avl.add(data[i]);
		}
		BinaryTrees.println(avl);
		for (int i = 0; i < data.length; i++) {
			avl.remove(data[i]);
			System.out.println("----------------------------");
			System.out.println("【" + data[i] + "】");
			BinaryTrees.println(avl);
		}
	}
}

B树

理解

B树是一种 平衡的多路搜索树，多用于文件系统、数据库的实现

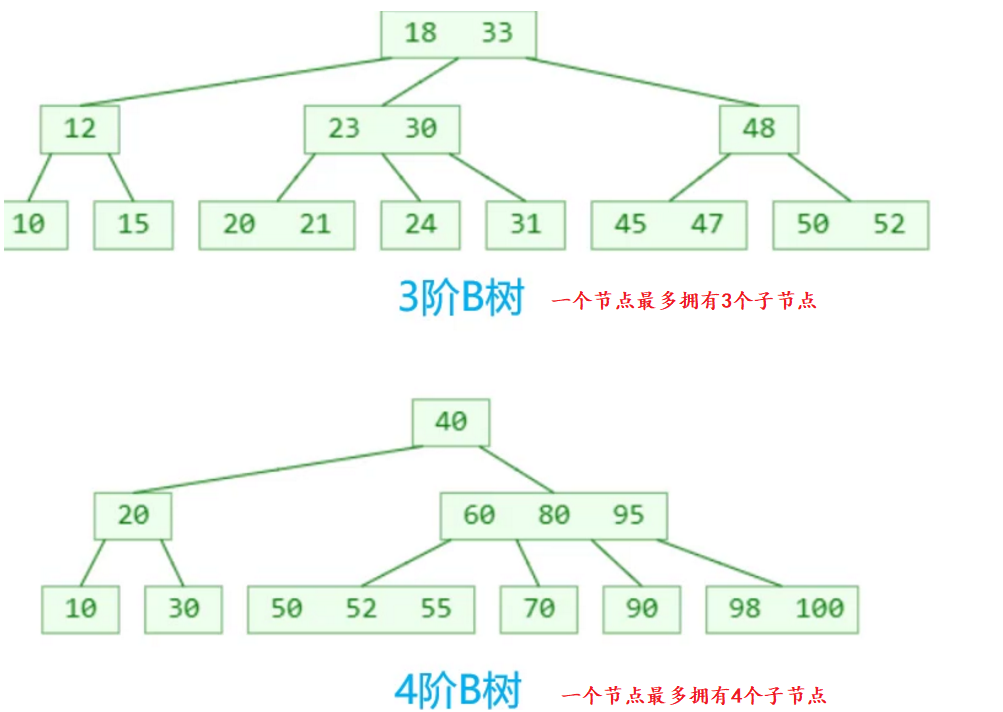
仔细观察B树，有什么眼前一亮的特点？

1 个节点可以存储超过 2 个元素、可以拥有超过 2 个子节点
拥有二叉搜索树的一些性质
平衡，每个节点的所有子树高度一致
比较矮

数据库中一般使用 200 ~ 300 阶B树

m阶B树的性质

规定的B树必须要遵守的一些性质

假设一个节点存储的元素个数为 x

根节点：1 ≤ x ≤ m − 1
非根节点：┌ m/2 ┐ − 1 ≤ x ≤ m − 1 （┌ ┐ => 向上取整）
如果有子节点，子节点个数：y = x + 1
- 根节点：2 ≤ y ≤ m
- 非根节点：┌ m/2 ┐ ≤ y ≤ m
  ➢ 比如 m = 3，2 ≤ y ≤ 3，因此可以称为（2, 3）树、2-3树
  ➢ 比如 m = 4，2 ≤ y ≤ 4，因此可以称为（2, 4）树、2-3-4树
  ➢ 比如 m = 5，3 ≤ y ≤ 5，因此可以称为（3, 5）树
  ➢ 比如 m = 6，3 ≤ y ≤ 6，因此可以称为（3, 6）树
  ➢ 比如 m = 7，4 ≤ y ≤ 7，因此可以称为（4, 7）树

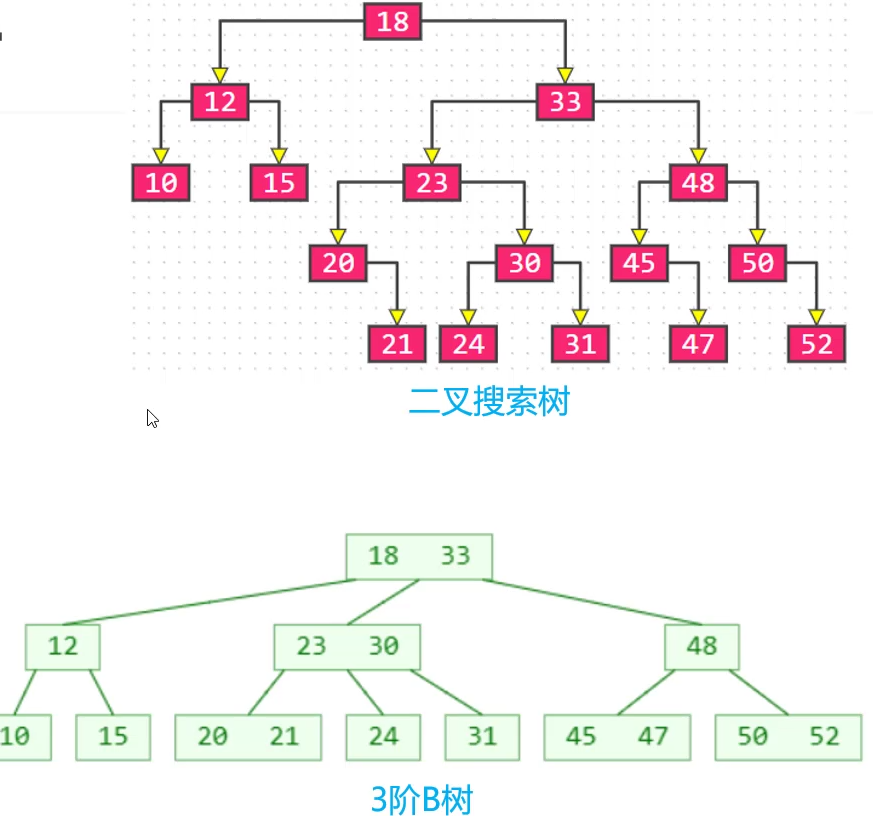
B树与二叉搜索树的关系

B树和二叉搜索树，在逻辑上是等价的

多代节点合并，可以获得一个 超级节点

2代合并的超级节点，最多拥有 4 个子节点（至少是 4阶B树）
3代合并的超级节点，最多拥有 8 个子节点（至少是 8阶B树）
n代合并的超级节点，最多拥有 2^n 个子节点（至少是 2^n 阶B树）

m阶B树，最多需要 log2m 代合并

B树搜索

跟二叉搜索树的搜索类似

先在节点内部从小到大开始搜索元素
如果命中，搜索结束
如果未命中，再去对应的子节点中搜索元素，重复步骤 1

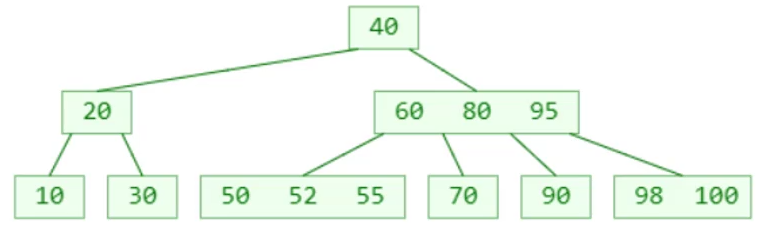
B树添加

新添加的元素必定是添加到叶子节点中 √ 红黑树会用到这个结论

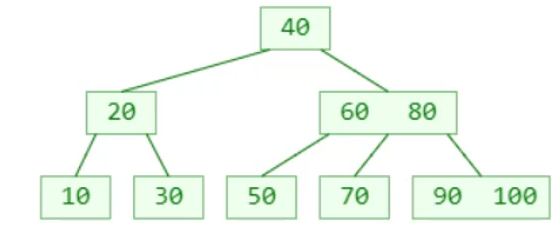
插入55
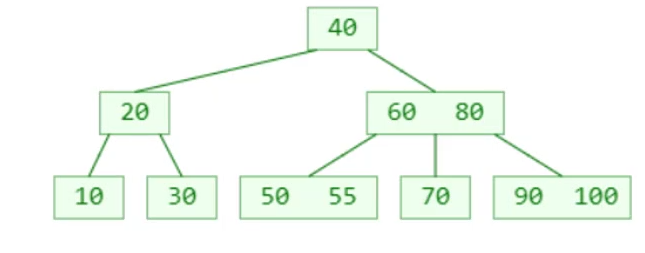
插入98

再插入 98 呢？（假设这是一棵 4阶B树）
- 最右下角的叶子节点的元素个数将超过限制
- 这种现象可以称之为：上溢（overflow）

添加 – 上溢的解决(假设5阶)

上溢节点的元素个数必然等于 m
假设上溢节点最中间元素的位置为 k
- 将 k 位置的元素向上与父节点合并
- 将 [0, k-1] 和 [k + 1, m - 1] 位置的元素分裂成 2 个子节点
  - 这 2 个子节点的元素个数，必然都不会低于最低限制（┌ m/2 ┐ − 1）
一次分裂完毕后，有可能导致父节点上溢，依然按照上述方法解决
- 最极端的情况，有可能一直分裂到根节点。如果一直传播到根节点就会导致B树变高(仅此一种情况导致B树变高)

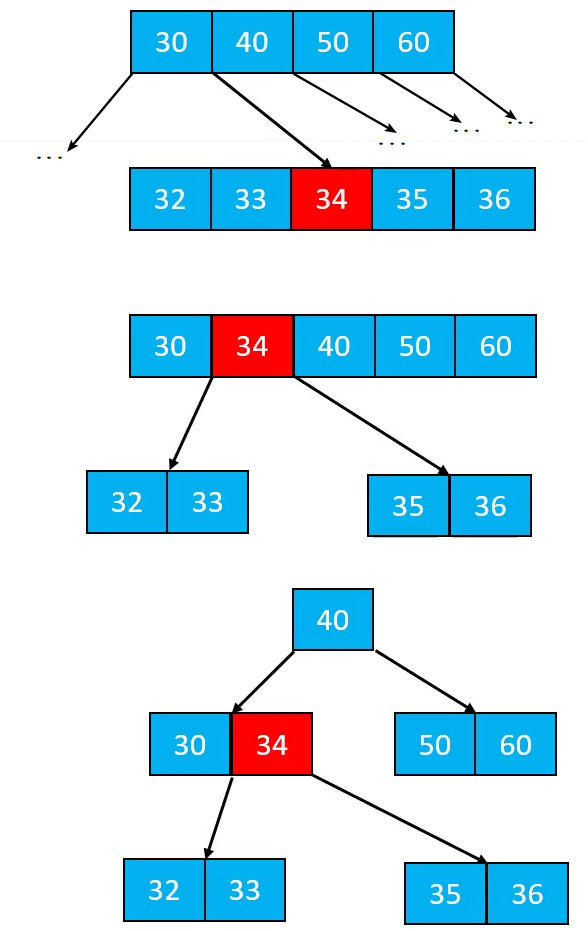
插入98

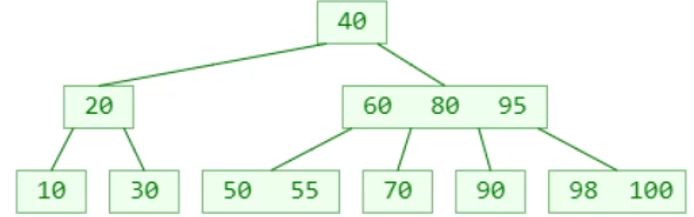
插入52

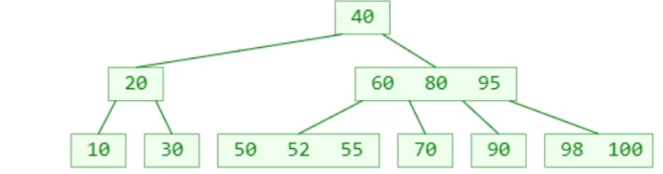
插入54

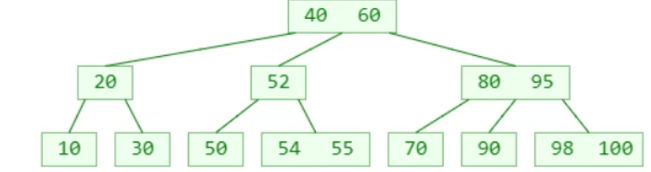
B树删除

如果需要删除的元素在叶子节点中，那么直接删除即可

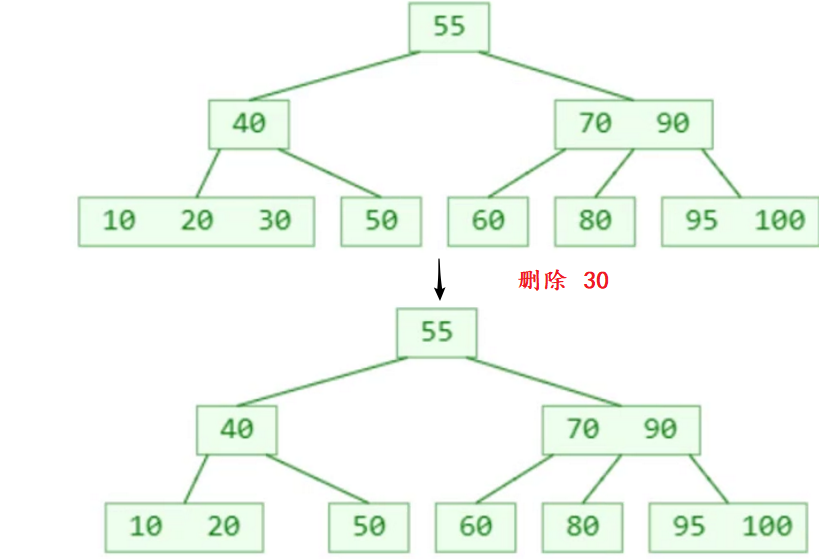
如果需要删除的元素在非叶子节点中

先找到前驱或后继元素，覆盖所需删除元素的值
再把前驱或后继元素删除

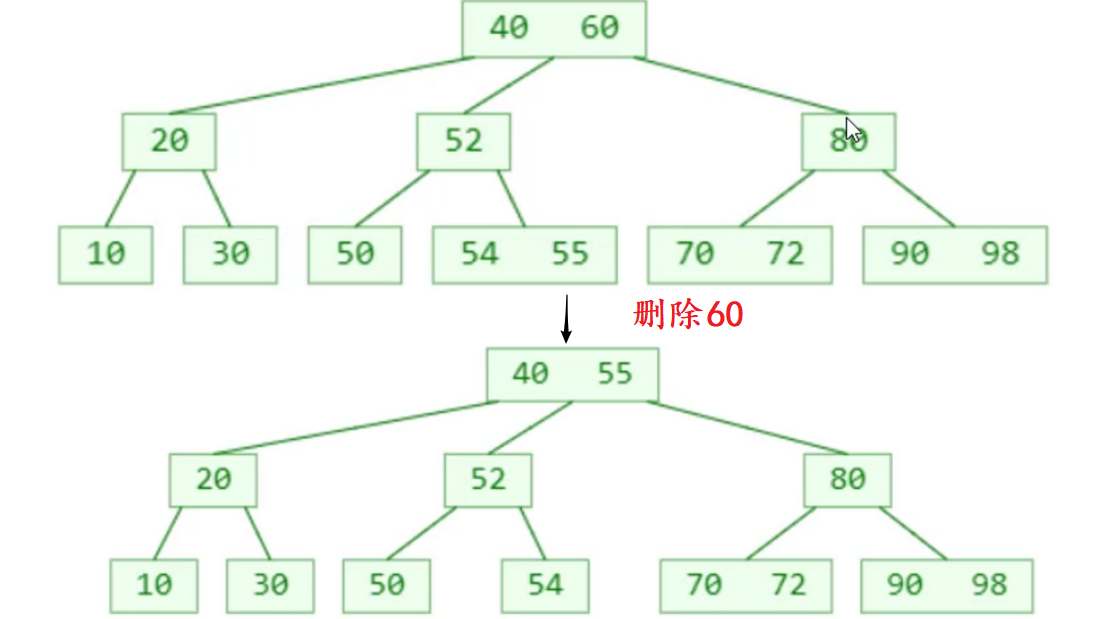
非叶子节点 的前驱或后继元素，必定在 叶子节点 中
- 所以这里的删除前驱或后继元素，就是最开始提到的情况：删除的元素在叶子节点中
- 真正的删除元素都是发生在叶子节点中 √红黑树会用到这个结论

删除-非叶子节点的下溢现象

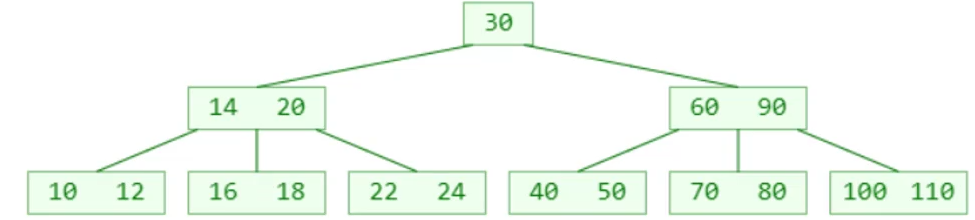
删除 22 ？（假设这是一棵 5阶B树）
- 叶子节点被删掉一个元素后，元素个数可能会低于最低限制( 即┌ m/2 ┐−1 )
- 这种现象称为：**下溢（underflow）**

删除-非叶子节点的下溢解决

下溢节点的元素数量必然等于 **┌ m/2 ┐ − 2**
如果下溢节点临近的兄弟节点，有至少 **┌ m/2 ┐** 个元素，可以向其借一个元素
- 将父节点的元素 **b** 插入到下溢节点的 **0** 位置（最小位置）
- 用兄弟节点的元素 **a**（最大的元素）替代父节点的元素 b
- 这种操作其实就是：**旋转**

注意：因为 b > a，所以不能破环二叉搜索树的性质直接将a放到下溢节点去。

如果下溢节点临近的兄弟节点，只有 **┌ m/2 ┐ − 1** 个元素
将父节点的元素 b 挪下来跟左右子节点进行合并
合并后的节点元素个数等于**┌ m/2 ┐ + ┌ m/2 ┐ − 2**，不会超过 **m − 1** 上溢
这个操作可能会导致父节点下溢，依然按照上述方法解决，下溢现象可能会一直往上传播。如果一直传播到根节点就会导致B树变矮(仅此一种情况导致B树变矮)

理解4阶b树

"理解了4阶b树，将能更好的学习理解红黑树"

4阶B树的性质

所有节点能存储的元素个数 x ：1 ≤ x ≤ 3
所有非叶子节点的子节点个数 y ：2 ≤ y ≤ 4

添加

手绘从 1 添加到 22

删除

手绘从 1 删除到 22

红黑树

理解

红黑树也是一种 自平衡的二叉搜索树，以前也叫做平衡二叉B树（Symmetric Binary B-tree）。

**红黑树必须满足以下 5 条性质 **

节点是 RED 或者 BLACK
根节点是 BLACK
叶子节点（外部节点，空节点）都是 BLACK
RED 节点的子节点都是 `BLACK
- RED 节点的 parent 都是 BLACK
- 从根节点到叶子节点的所有路径上不能有 2 个连续的 RED 节点
从任一节点到叶子节点的所有路径都包含 相同数目 的 BLACK 节点

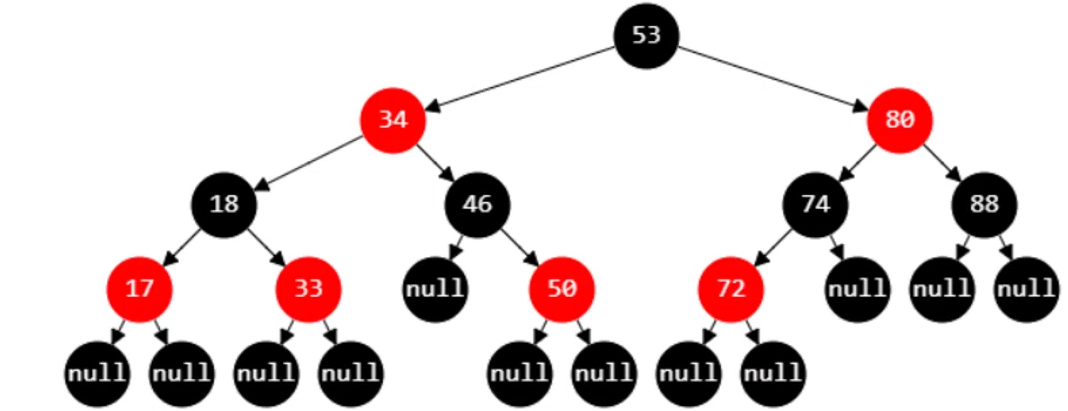
注意：红黑树的 叶子节点 是让原来度为 0 的节点或度为 1 的节点都变成度为 2 的节点后的叶子节点。（增加空节点 null 实现此功能）此时红黑树就变成了真二叉树。

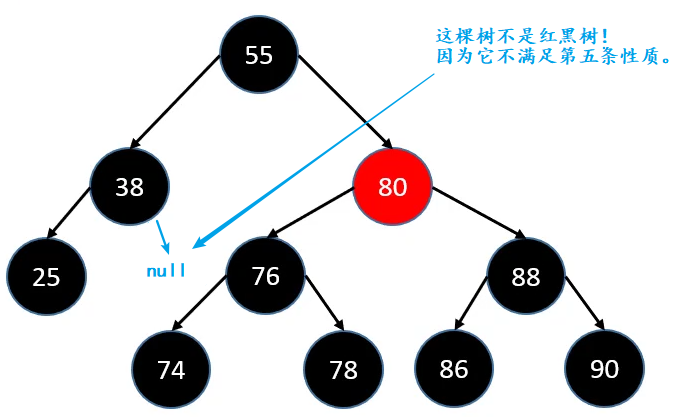
注意：之后展示的红黑树都会省略 null 节点（空节点是假想出来的）

红黑树的平衡 （为什么满足以上5条性质，就能保证红黑树是平衡的？）

以上5条性质，可以保证红黑树等价于 4阶B树
相比AVL树，红黑树的平衡标准比较宽松：没有一条路径会大于其他路径的2倍
可以理解为是一种弱平衡、黑高度平衡 (任意一条路的黑节点数量都是相等的)
红黑树的最大高度是 2 ∗ log(n + 1) ，依然是 O(logn) 级别

红黑树的平均时间复杂度

搜索：O(logn)
添加：O(logn)，O(1) 次的旋转操作
删除：O(logn)，O(1) 次的旋转操作

AVL树对比红黑树

AVL树
- 平衡标准比较严格：每个左右子树的高度差不超过1
- 最大高度是 1.44 ∗ log(n + 2) − 1.328（100W个节点，AVL树最大树高28）
- 搜索、添加、删除都是 O(logn) 复杂度，其中添加仅需 O(1) 次旋转调整、删除最多需要 O(logn) 次旋转调整
红黑树
- 平衡标准比较宽松：没有一条路径会大于其他路径的2倍
- 最大高度是 2 ∗ log(n + 1)（ 100W个节点，红黑树最大树高40）
- 搜索、添加、删除都是 O(logn) 复杂度，其中添加、删除都仅需 O(1) 次旋转调整
搜索的次数远远大于插入和删除，选择AVL树；搜索、插入、删除次数几乎差不多，选择红黑树
相对于AVL树来说，红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作，整体来说性能要优于AVL树
红黑树的平均统计性能优于AVL树，实际应用中更多选择使用红黑树

红黑树的等价变换

红黑树和四阶B树(2-3-4树）具有等价性

BLACK 节点与它的 RED 子节点融合在一起，形成1个B树节点

红黑树的 BLACK 节点个数与 4阶B树的节点总个数相等

注意：用 2-3树与红黑树进行类比，这是极其不严谨的，2-3树并不能完美匹配红黑树的所有情况

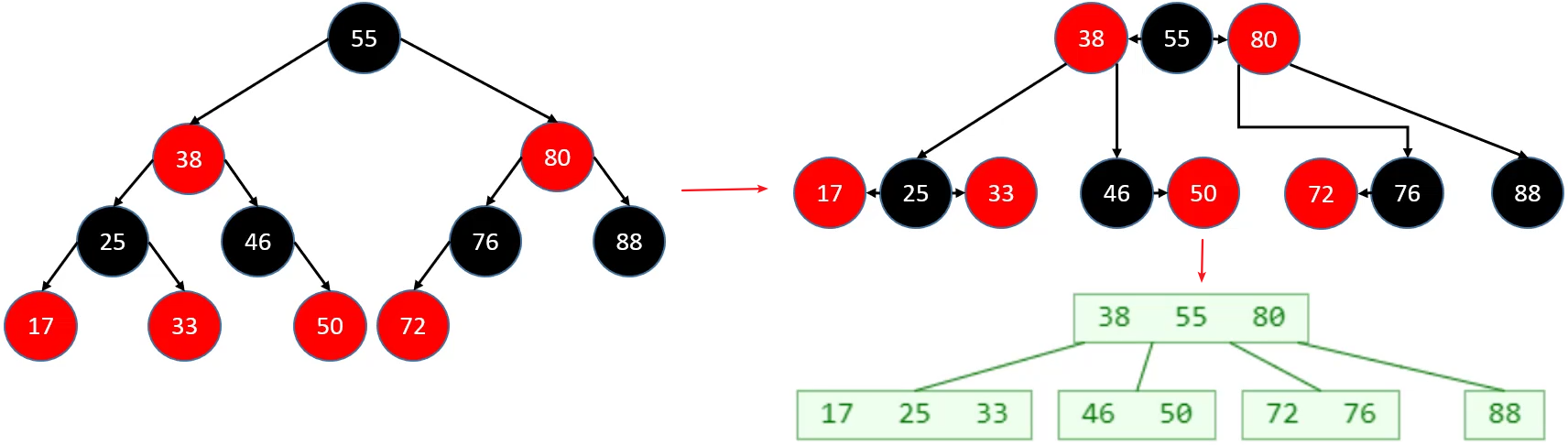
红黑树与 2-3-4树的比较

如果下图最底层的 BLACK 节点是不存在的，在B树中是什么样的情形？=>整棵B树只有1个节点，而且是超级节点

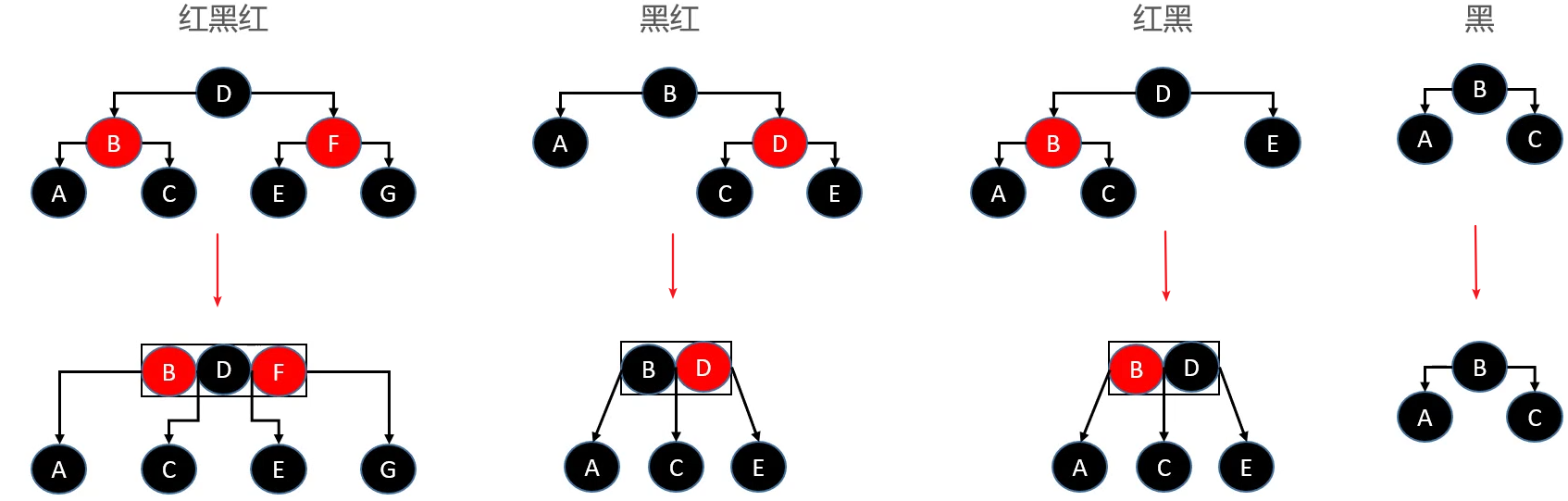
添加节点

已知：

B树中，新元素必定是添加到叶子节点中
4阶B树所有节点的元素个数 x 都符合 1 ≤ x ≤ 3

注意：
① 建议新添加的节点默认为 RED，这样能够让红黑树的性质尽快满足(性质1，2，3，5 都满足，性质 4 不一定)
② 如果添加的是根节点，染成 BLACK 即可

添加的所有情况

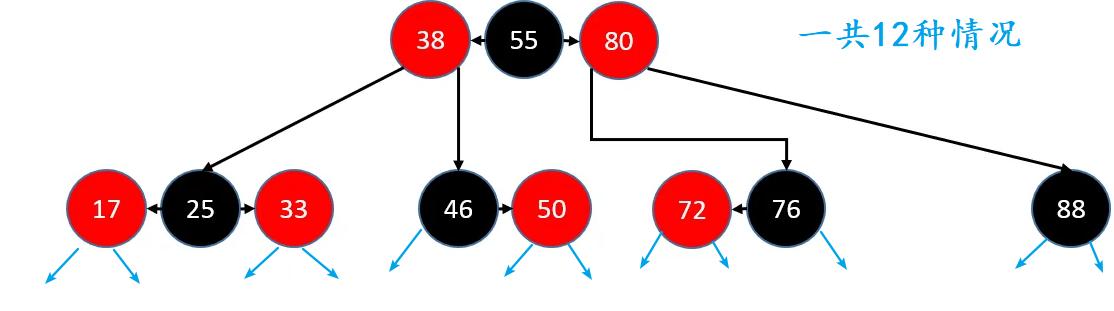
有 4 种情况既满足红黑树的性质四：parent 为 BLACK，同时也满足4阶B树的性质，因此不用做任何额外的处理。

有 8 种情况不满足红黑树的性质四：parent 为 RED（ Double Red ），其中前 4 种属于B树节点上溢的情况

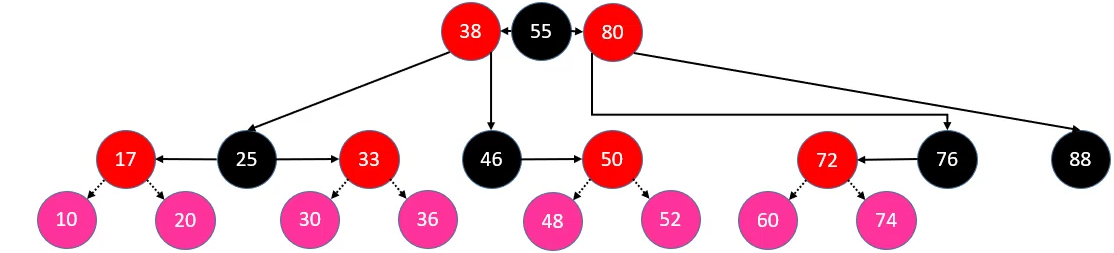
添加 – 修复性质4 – LL\RR

判定条件：uncle 不是 RED

parent 染成 BLACK，grand 染成 RED
grand 进行单旋操作：
- LL：右旋转
- RR：左旋转

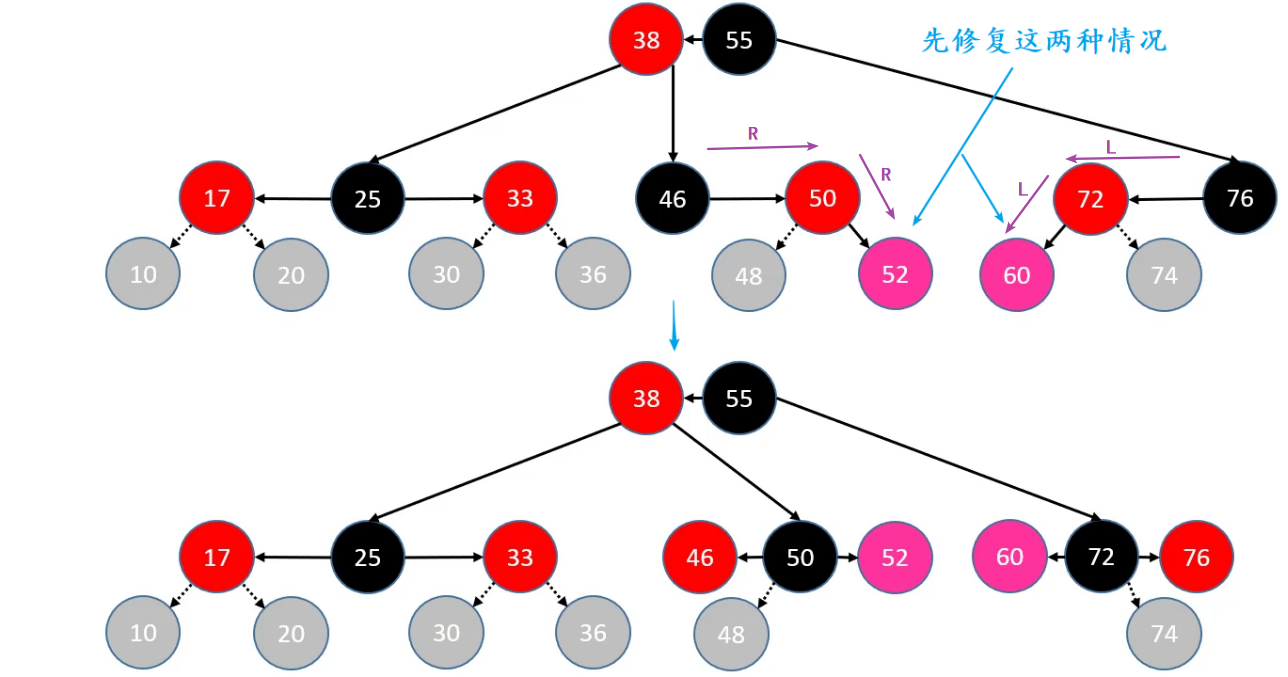
添加 – 修复性质4 – LR\RL

判定条件：uncle 不是 RED

自己染成 BLACK，grand 染成 RED
进行双旋操作：
- LR：parent 左旋转， grand 右旋转
- RL：parent 右旋转， grand 左旋转

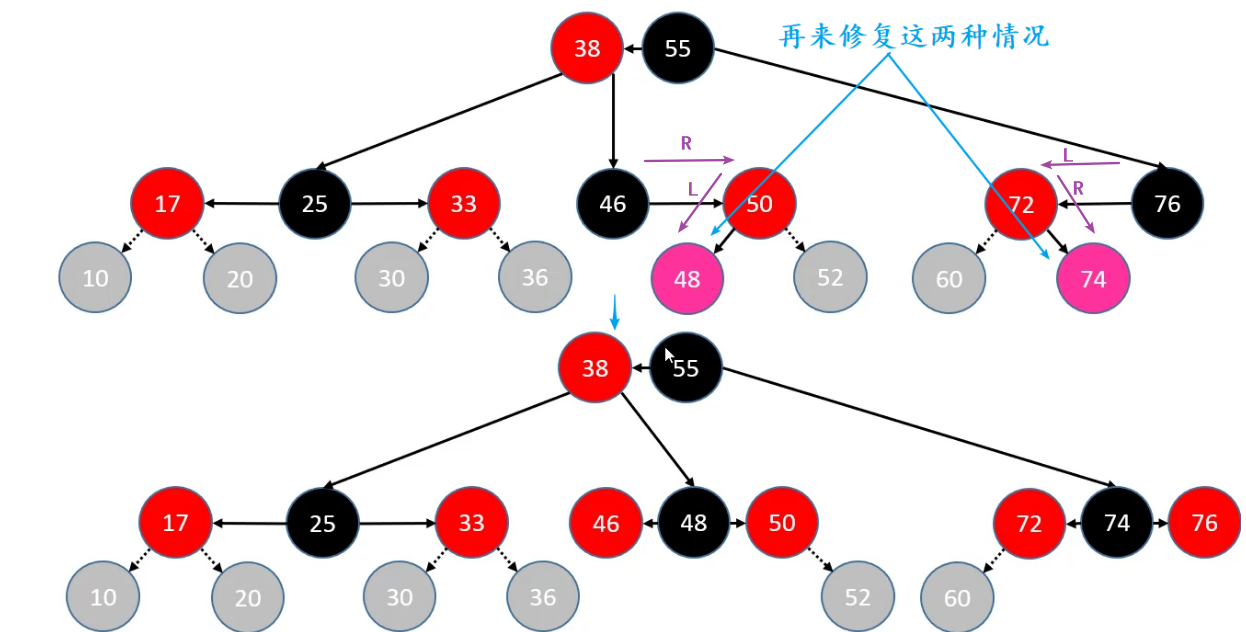
添加 – 修复性质4 – 上溢 – LL

注意：之前修复的四种情况，添加节点的叔父节点都为null(null默认记为黑色)。

判定条件：uncle 是 RED

parent、uncle 染成 BLACK
grand 向上合并，且染成 RED，当做是新添加的节点进行处理

grand 向上合并时，可能继续发生上溢

若上溢持续到根节点，只需将根节点染成 BLACK

添加 – 修复性质4 – 上溢 – RR

判定条件：uncle 是 RED

parent、uncle 染成 BLACK
grand 向上合并，且染成 RED，当做是新添加的节点进行处理

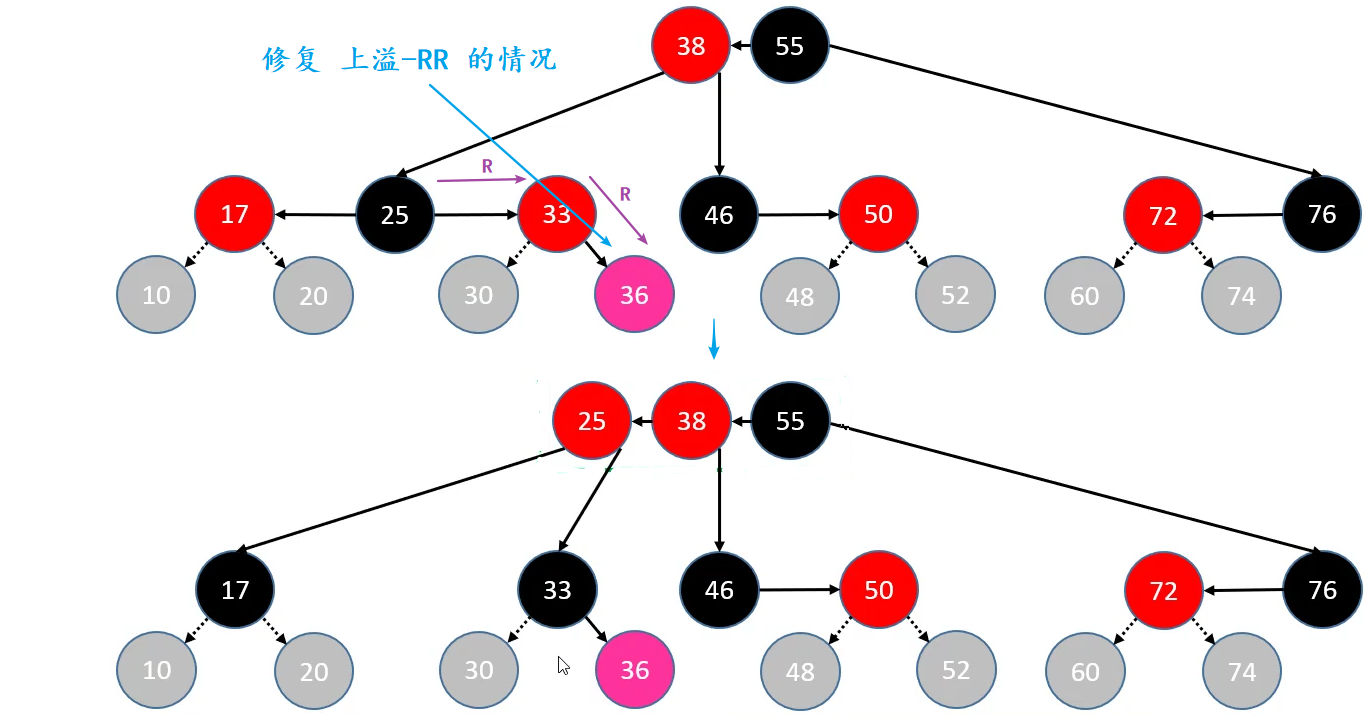
添加 – 修复性质4 – 上溢 – LR

判定条件：uncle 是 RED

parent、uncle 染成 BLACK
grand 向上合并，且染成 RED，当做是新添加的节点进行处理

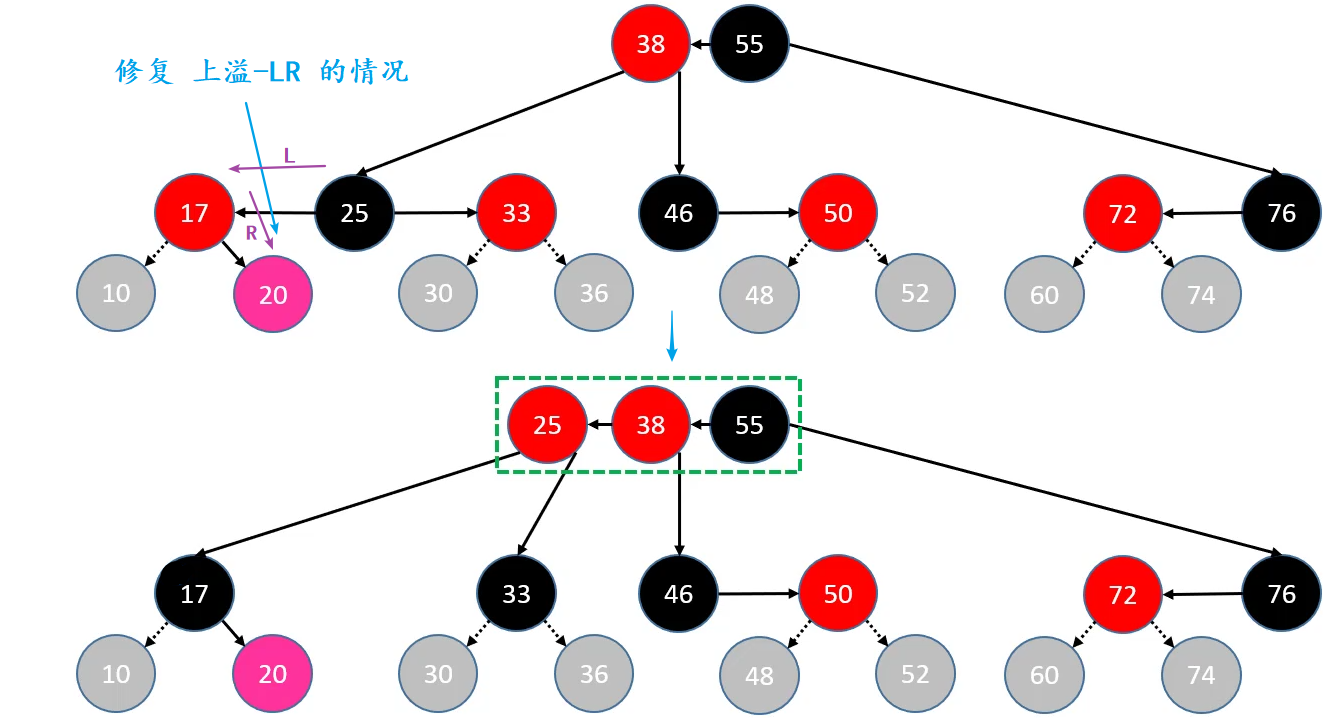
添加 – 修复性质4 – 上溢 – RL

判定条件：uncle 是 RED

parent、uncle 染成 BLACK
grand 向上合并，且染成 RED，当做是新添加的节点进行处理

删除节点

已知：B树中，最后真正被删除的元素都在叶子节点中

删除-RED节点

直接删除，不用做任何调整

删除 – BLACK 节点 （有 3 种情况）

删除拥有 2 个 RED 子节点的 BLACK 节点（如 25）

不可能被直接删除，因为会找它的前驱节点或后继节点替代删除，在BSTree中已经实现了此功能因此也不用考虑这种情况

删除拥有 1 个 RED 子节点的 BLACK 节点（如 46，76）

删除 BLACK 叶子节点（如 88）

总结：删除后真正需要处理的只有两种情况：① 删除拥有 1 个 RED 子节点的 BLACK 节点 ② 删除 BLACK 叶子节点

删除 - 拥有 1 个 RED 子节点的 BLACK 节点

判定条件：用以替代的子节点是 RED “注意：删除Black叶子节点，没有用于替代的就相当于用null(默认为Black)替代”

将替代的子节点染成 BLACK 即可保持红黑树性质

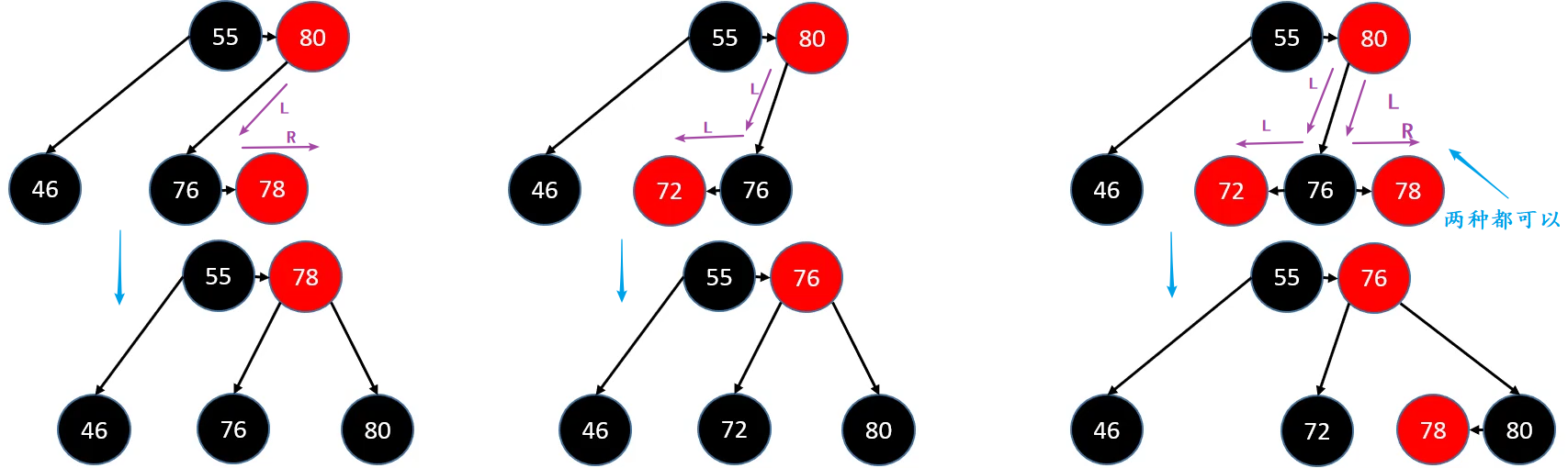
删除 - BLACK 叶子节点 - sibling为 BLACK

BLACK 叶子节点被删除后，会导致B树节点下溢（比如删除88）

判定条件：如果 sibling 至少有 1 个 RED 子节点

进行旋转操作
旋转之后的中心节点继承 parent 的颜色
旋转之后的左右节点染为 BLACK

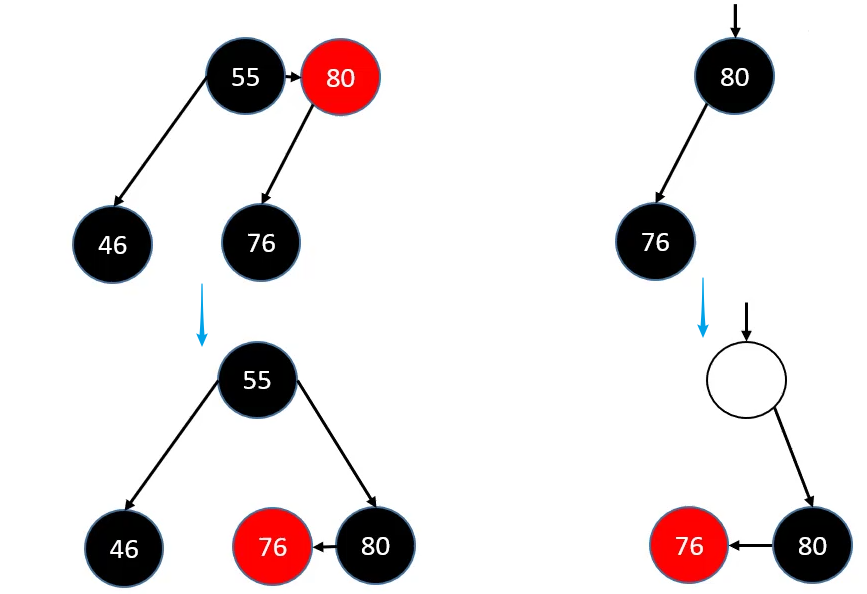
判定条件：如果 sibling 没有 RED 子节点

将 sibling 染成 RED、parent 染成 BLACK 即可修复红黑树性质（合并）
如果 parent 是 BLACK 会导致 parent 也下溢，这时只需要把 parent 当做被删除的节点处理即可（递归）

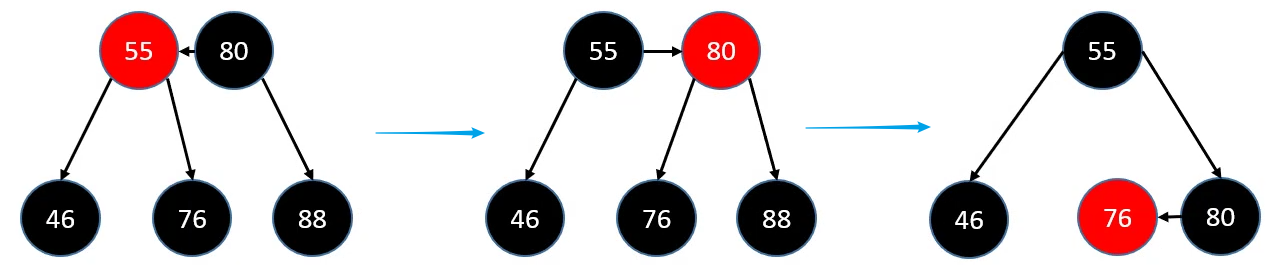
删除 - BLACK 叶子节点 - sibling为 RED

如果 sibling 是 RED

sibling 染成 BLACK，parent 染成 RED，进行旋转
于是又回到 sibling 是 *BLACK 的情况

实现

/**
 * @Description 红黑树
 * @author Polaris
 * @version
 * @date 2020年3月10日下午8:35:16
 */
public class RBTree<E> extends BBSTree<E>{
	private static final boolean RED = false;
	private static final boolean BLACK = true;
	
	public RBTree() {
		this(null);
	}

	public RBTree(Comparator<E> comparator) {
		super(comparator);
	}
	
	/**
	 * RB树特有的节点
	 */
	private static class RBNode<E> extends Node<E> {
		boolean color = RED;
		public RBNode(E element, Node<E> parent) {
			super(element, parent);
		}
		
		@Override
		public String toString() {
			String str = "";
			if(color == RED) {
				str = "R_";
			}
			return str + element.toString();
		}
	}
	
	@Override
	protected Node<E> createNode(E element, Node<E> parent) {
		return new RBNode<E>(element,parent);
	}
	
	/**
	 * 给节点上色
	 */
	private Node<E> color(Node<E> node,boolean color) {
		if(node == null) return node;
		((RBNode<E>)node).color = color;
		return node;
	}
	
	/**
	 * 将节点染成红色
	 */
	private Node<E> red(Node<E> node){
		return color(node,RED);
	}
	
	/**
	 * 将节点染成黑色
	 */
	private Node<E> black(Node<E> node){
		return color(node,BLACK);
	}
	
	/**
	 * 获取当前节点的颜色
	 */
	private boolean colorOf(Node<E> node) {
		return node == null ? BLACK : ((RBNode<E>)node).color;
	}
	
	/**
	 * 判断当前颜色是否为黑色
	 */
	private boolean isBlack(Node<E> node) {
		return colorOf(node) == BLACK;
	}
	
	/**
	 * 判断当前颜色是否为红色
	 */
	private boolean isRed(Node<E> node) {
		return colorOf(node) == RED;
	}

	/**
	 * 	实现添加新节点后的处理操作
	 */
	@Override
	protected void afterAdd(Node<E> node) {
		Node<E> parent = node.parent;
		//添加的是根节点 或 上溢到根节点
		if(parent == null) {
			black(node);
			return;
		}
		//类型一：parent是黑色（不用处理四种情况）
		if(isBlack(parent)) return;
		//类型二：parent是红色且uncle是红色（会上溢的四种情况）
		Node<E> uncle = parent.getSibling();
		Node<E> grand = red(parent.parent);//以下情况都需要将grand染成红色，可以统一处理
		if(isRed(uncle)) {
			black(parent);
			black(uncle);
			//把祖父节点当作是新添加的节点
			afterAdd(grand);//上溢递归调用
			return;
		}
		//类型三：parent是红色且uncle不是红色（需要旋转的四种情况）
		if(parent.isLeftChild()) {//L
			if(node.isLeftChild()) { //LL
				black(parent);
			} else { //LR
				black(node);
				rotateLeft(parent);
			}
			rotateRight(grand);
		} else { //R
			if(node.isLeftChild()) { //RL
				black(node);
				rotateRight(parent);
			} else { //RR
				black(parent);
			}
			rotateLeft(grand);
		}
	}
	
	/**
	 * 	实现删除节点后的处理操作
	 */
	@Override
	protected void afterRemove(Node<E> node,Node<E> replacement) {
		//情况一：如果删除的节点是红色，不用处理
		if(isRed(node)) return;
		//情况二：用于取代node子节点的是红色节点
		if(isRed(replacement)) {
			black(replacement);
			return;
		}
		//情况三：删除的是黑色叶子节点（下溢）
		Node<E> parent = node.parent;
		//删除的是根节点
		if(parent == null) return;
		//判断被删除的node的节点是左还是右
		boolean left = parent.left == null || node.isLeftChild();
		Node<E> sibling = left ? parent.right : parent.left;
		if(left) { //被删除的节点在左边，兄弟节点在右边(镜像对称处理)
			if(isRed(sibling)) { //兄弟节点是红色，就要转成黑色
				black(sibling);
				red(parent);
				rotateLeft(parent);
				//更换兄弟
				sibling = parent.right;
			}
			//兄弟节点必然是黑色
			if(isBlack(sibling.left) && isBlack(sibling.right)) {
				//兄弟节点没有一个红色子节点，父节点要向下向子节点合并
				boolean parentBlack = isBlack(parent);
				black(parent);
				red(sibling);
				if(parentBlack) {
					afterRemove(parent, null);
				}
			} else { //兄弟节点至少有 1 个红色节点,就要向兄弟节点借元素
				if(isBlack(sibling.right)) {
					//兄弟节点的右边不是红色，则兄弟要先旋转
					rotateRight(sibling);
					sibling = parent.right;
				}
				color(sibling,colorOf(parent));
				black(sibling.right);
				black(parent);
				rotateLeft(parent);
			}
		} else { //被删除的节点在右边，兄弟节点在左边（图示的是这种）
			if(isRed(sibling)) { //兄弟节点是红色，就要转成黑色
				black(sibling);
				red(parent);
				rotateRight(parent);
				//更换兄弟
				sibling = parent.left;
			}
			//兄弟节点必然是黑色
			if(isBlack(sibling.left) && isBlack(sibling.right)) {
				//兄弟节点没有一个红色子节点，父节点要向下向子节点合并
				boolean parentBlack = isBlack(parent);
				black(parent);
				red(sibling);
				if(parentBlack) {
					afterRemove(parent, null);
				}
			} else { //兄弟节点至少有 1 个红色节点,就要向兄弟节点借元素
				if(isBlack(sibling.left)) {
					//兄弟节点的左边不是红色，则兄弟要先旋转
					rotateLeft(sibling);
					sibling = parent.left;
				}
				color(sibling,colorOf(parent));
				black(sibling.left);
				black(parent);
				rotateRight(parent);
			}
		}
	}
	
}

测试

public class RBTreeTest {
	//添加测试
	@Test
	public void test() {
		Integer[] data = new Integer[] {
				55,87,56,74,96,22,62,20,70,68,90,50};
		RBTree<Integer> rb = new RBTree<>();
		for (int i = 0; i < data.length; i++) {
			rb.add(data[i]);
			System.out.println("----------------------------");
			System.out.println("【" + data[i] + "】");
			BinaryTrees.println(rb);
		}
		BinaryTrees.println(rb);
	}
	
	//删除测试
	@Test
	public void test1() {
		Integer[] data = new Integer[] {
				55,87,56,74,96,22,62,20,70,68,90,50};
		RBTree<Integer> rb = new RBTree<>();
		for (int i = 0; i < data.length; i++) {
			rb.add(data[i]);
		}
		BinaryTrees.println(rb);
		for (int i = 0; i < data.length; i++) {
			rb.remove(data[i]);
			System.out.println("----------------------------");
			System.out.println("【" + data[i] + "】");
			BinaryTrees.println(rb);
		}
	}
}