哈希表
哈希表
理解
哈希表也叫做 散列表( hash 有“剁碎”的意思)
它是如何实现高效处理数据的?
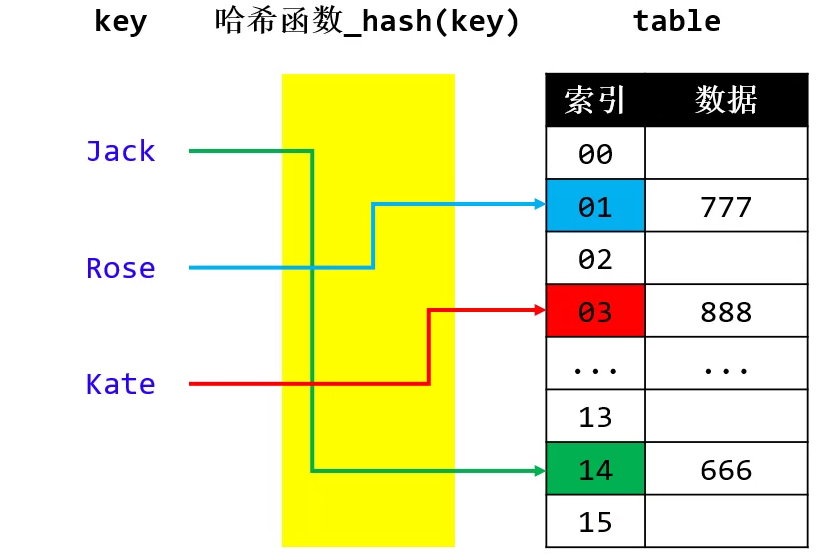
put("Jack", 666);
put("Rose", 777);
put("Kate", 888);
添加、搜索、删除的流程都是类似的
利用哈希函数生成 key 对应的 index【O(1)】
根据 index 操作定位数组元素【O(1)】
哈希表是【空间换时间】的典型应用
哈希函数,也叫做 散列函数
哈希表内部的数组元素,很多地方也叫 Bucket(桶),整个数组叫 Buckets 或者 Bucket Array
注意:在实际应用中很多时候的需求:Map 中存储的元素不需要讲究顺序,Map 中的 Key 不需要具备可比较性。其实不考虑顺序、不考虑 Key 的可比较性,Map 有更好的实现方案,平均时间复杂度可以达到 O(1) ,那就是采取
哈希表来实现 Map
哈希冲突(Hash Collision)
哈希冲突也叫做 哈希碰撞
- 2 个不同的 key,经过哈希函数计算出相同的结果
- key1 ≠ key2 ,hash(key1) = hash(key2)

解决哈希冲突的常见方法
开放定址法(Open Addressing)即按照一定规则向其他地址探测,直到遇到空桶 。再哈希法(Re-Hashing)即设计多个哈希函数链地址法(Separate Chaining)即比如通过链表将同一index的元素串起来
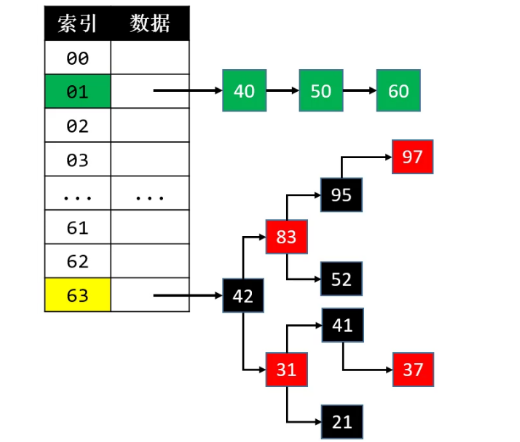
JDK1.8的哈希冲突解决方案
- 默认使用
单向链表将元素串起来(链地址法) - 在添加元素时,可能会由
单向链表转为红黑树来存储元素。比如当哈希表容量 ≥ 64 且 单向链表的节点数量大于 8 时 - 当
红黑树节点数量少到一定程度时,又会转为单向链表 - JDK1.8中的哈希表是使用
链表+红黑树解决哈希冲突 - 思考一下这里为什么使用单链表?=> 每次都是从头节点开始遍历,单向链表比双向链表少一个指针,可以节省内存空间
哈希函数
哈希表中哈希函数的实现步骤大概如下:
先生成
key 的哈希值(必须是整数)再让
key 的哈希值跟数组的大小进行相关运算,生成一个索引值
public int hash(Object key) {
return hash_code(key) % table.length;
}为了提高效率,可以使用 & 位运算取代 % 运算【前提:将数组的长度设计为 2 的幂(2^n)】
public int hash(Object key) {
return hash_code(key) & (table.length - 1);
}
// 1 = 2^0
// 10 = 2^1
// 100 = 2^2
// 1000 = 2^3
// 10000 = 2^4
// 01111 = 2^4 - 1 = 1111
// ==> table.length - 1 表示 & 一个全为1的二进制数。结果必然小与这个全为1的二进制数
// 假设哈希值为1001010 =>
// 1001010
// & 0001111
// ----------
// 0001010 => 生成的值的范围是 0000 ~ 1111良好的哈希函数 能让哈希值更加均匀分布 → 减少哈希冲突次数 → 提升哈希表的性能
此外,hashCode相等,生成的索引不一定相等。
11000
&111
------
000
10000
&111
------
000如何生成key的哈希值
key 的常见种类可能有
整数、浮点数、字符串、自定义对象
不同种类的 key,哈希值的生成方式不一样,但目标是一致的
尽量让每个 key 的哈希值是唯一的
尽量让 key 的所有信息参与运算
在Java中,HashMap 的 key 必须实现 hashCode、equals 方法,也允许 key 为 null
整数
整数值当做哈希值
比如 10 的哈希值就是 10
public static int hashCode(int value) {
return value;
}浮点数
将存储的二进制格式转为整数值
public static int hashCode(float value) {
return Float.floatToIntBits(value);
}long
注意:Java的哈希值必须是
int类型(32位)
public static int hashCode(long value) {
//如果强制转换为int会直接砍掉前面32位,不推荐
return (int)(value ^ (value >>> 32));
}
// 注意:>>> 和 ^ 的作用是?(>>>是无符号右移,^是异或运算)
// ① 高32bit 和 低32bit 混合计算出 32bit 的哈希值
// ② 充分利用所有信息计算出哈希值
// 另外:为什么不用 & 或者 |而是用 ^ ?
// ① 如果value前32位全为1,使用 & 运算后32位就相当于没算了。
// ② 如果value前32位全为1,使用 | 运算后32位就全为1了。
double
public static int hashCode(double value) {
long bits = doubleToLongBits(value);
return (int)bits ^ (bits >>> 32);
}字符串
先看一个问题:整数 5489 是如何计算出来的?
5 ∗ 10^3 + 4 ∗ 10^2 + 8 ∗ 10^1 + 9 ∗ 10^0字符串是由若干个字符组成的
- 比如字符串 jack,由 j、a、c、k 四个字符组成(字符的本质就是一个整数,ASCII码)
- 因此,jack 的哈希值可以表示为 j ∗ n^3 + a ∗ n^2 + c ∗ n^1 + k ∗ n^0,等价于 [ ( j ∗ n + a ) ∗ n + c ] ∗ n + k (等价后可以避免n的重复计算)
- 在JDK中,乘数 n 为 31,为什么使用 31? => 31 是一个奇素数,JVM会将 31 * i 自动优化转化为 (i << 5) – i
注意:
① 31 * i = (2^5 - 1) * i = i * 2^5 - i = (i << 5) - i
② 31不仅仅是符合2^n - 1,它也是一个奇素数(既是奇数,也是质数。即质数)
=>素数和其他数相乘的结果比其他方式更容易产生唯一性,减少哈希冲突。
@Test
public void StrHashTest() {
String str = "jack";
int len = str.length();
int hashCode = 0;
for(int i = 0;i < len;i++) {
char c = str.charAt(i);
//hashCode = (hashCode << 5) - hashCode + c;
hashCode = hashCode * 31 + c;
// [ ( j ∗ n + a ) ∗ n + c ] ∗ n + k
}
System.out.println(hashCode);//3254239
System.out.println(str.hashCode());//3254239
}总结
@Test
public void hashTest() {
int a = 110;
float b = 10.6f;
long c = 156l;
double d = 10.9;
String e = "rose";
System.out.println(Integer.hashCode(a));
System.out.println(Float.hashCode(b));
//System.out.println(Float.floatToIntBits(b)); //内部实现
System.out.println(Long.hashCode(c));
System.out.println(Double.hashCode(d));
System.out.println(e.hashCode());
}自定义对象的哈希值
自定义对象的hash值默认与该对象的内存地址有关。
注意:
① 哈希值太大,整型溢出怎么办? => 不用作任何处理,溢出了还是一个整 数。
② 不重写hashCode方法有什么后果? => 会以对象内存地址相关的值作为hash值。
重点:
① hashCode方法在在计算索引时调用
② equals方法在hash冲突时比较两个key是否相等时调用
④ 如果要求两个对象的哪些成员变量相等就代表这两个对象相等的话,hashCode方法和equals方法就只包含这些成员变量的计算就可以了。(hashCode方法必须要保证 equals 为 true 的 2 个key的哈希值一样,反过来hashCode相等的key,不一定equals为true)
public class HashTest {
@Test
public void PersonHashTest() {
Person p1 = new Person(15,"rose",58.5f);
Person p2 = new Person(15,"rose",58.5f);
//System.out.println(p1.hashCode());//1834188994
//System.out.println(p2.hashCode());//1174361318
//=>自定义对象hash值默认与对象的地址值有关
//√ 重写hashCode方法后:hash值相等意味着生成的索引相同
System.out.println(p1.hashCode());//185317790
System.out.println(p2.hashCode());//185317790
Map<Object,Object> map = new HashMap<>();
map.put(p1,"abc");
map.put(p2,"bcd");//如果p1与p2"相等",就会覆盖,此时size为1才合理。
//=>此时需要重写equals方法比较两个key是否"相等"
//√ 注意:不能通过hash值的比较来判断两个key"相等",因为可能两个
// 完全不同类型的key的hash值是相等的。
System.out.println(map.size());//1
}
}
class Person {
private int age;
private String name;
private float height;
public Person(int age, String name, float height) {
super();
this.age = age;
this.name = name;
this.height = height;
}
public Person() {
super();
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public float getHeight() {
return height;
}
public void setHeight(float height) {
this.height = height;
}
@Override
public String toString() {
return "Person [age=" + age + ", name="
+ name + ", height=" + height + "]";
}
/**
* 用来计算当前对象的hash值
*/
@Override
public int hashCode() {
//Integer.hashCode(age);
//Float.hashCode(height);
//name != null ? name.hashCode() : 0;
int hashCode = Integer.hashCode(age);
hashCode = hashCode * 31 + Float.hashCode(height);
hashCode = hashCode * 31 +
(name != null ? name.hashCode() : 0);
return hashCode;
}
/**
* 用来比较两个对象是否相等
*/
@Override
public boolean equals(Object obj) {
if(this == obj) return true;
//if(obj == null || obj instanceof Person) return false;
if(obj == null || obj.getClass() != getClass()) return false;
Person p = (Person)obj;
return p.age == age
&& p.height == height
&& p.name == null ? name == null : p.name.equals(name);
}
}HashMap实现
这里有如下设计
- 直接使用红黑树解决hash冲突
- 数组元素存储红黑树根节点,而不是存储红黑树对象。这样做的好处是就不用额外存储红黑树的size,comparator属性了(用不上)。
/**
* @Description hashMap, hash冲突直接使用红黑树解决
* @Author monap
* @Date 2022/1/2 15:53
*/
@SuppressWarnings("unchecked")
public class HashMap<K, V> implements Map<K, V> {
// 所有节点的数量
private int size;
private static final boolean RED = false;
private static final boolean BLACK = true;
private Node<K, V>[] table;
private static final int DEFAULT_CAPACTIY = 1 << 4; // 默认容量
private static final float DEFAULT_LOAD_FACTOR = 0.75f; // 装填因子
protected static class Node<K, V> {
int keyHash;
K key;
V value;
boolean color = RED;
Node<K, V> left; // 左子节点
Node<K, V> right; // 右子节点
Node<K, V> parent; // 父节点
public Node(K key, V value, Node<K, V> parent) {
this.key = key;
int hash = key == null ? 0 : key.hashCode();
this.keyHash = hash ^ (hash >>> 16); // 扰动计算一次,使hash值排布更均匀
this.value = value;
this.parent = parent;
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
public boolean isLeftChild() {
return parent != null && this == parent.left;
}
public boolean isRightChild() {
return parent != null && this == parent.right;
}
public Node<K, V> getSibling() {
if (isLeftChild()) {
return parent.right;
}
if (isRightChild()) {
return parent.left;
}
return null;
}
@Override
public String toString() {
return "Node_" + key + "_" + value;
}
}
protected Node<K, V> createNode(K key, V value, Node<K, V> parent) {
return new Node<>(key, value, parent);
}
/**
* 获取key的hash值,并做一次扰动计算
*
* @param key
* @return
*/
private int hash(K key) {
if (key == null) return 0;
int hash = key.hashCode();
return hash ^ (hash >>> 16);
}
/**
* 根据key生成索引(在桶数组中的位置)
*
* @param key
* @return
*/
private int index(K key) {
return hash(key) & (table.length - 1);
}
/**
* 根据node获取索引(在桶数组中的位置)
*
* @param node
* @return
*/
private int index(Node<K, V> node) {
return node.keyHash & (table.length - 1);
}
public HashMap() {
table = new Node[DEFAULT_CAPACTIY];
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void clear() {
if (size == 0) return;
size = 0;
Arrays.fill(table, null);
}
@Override
public V put(K key, V value) {
// 检查是否需要扩容
resize();
int index = index(key);
// 取出index位置的红黑树根节点
Node<K, V> root = table[index];
if (root == null) {
root = createNode(key, value, null);
table[index] = root;
size++;
afterPut(root);
return null;
}
// hash冲突,添加新节点到红黑树
// 1.找到待添加位置的父节点
Node<K, V> parent = root;
Node<K, V> node = root;
int cmp = 0;
K k1 = key;
int h1 = hash(k1);
Node<K, V> result = null;
boolean searched = false;//是否已经搜索过这个key
do {
parent = node;
K k2 = node.key;
int h2 = node.keyHash;
// 增加规则,先比较hash值,提高效率
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (Objects.equals(k1, k2)) {
cmp = 0;
} else if (k1 != null && k2 != null
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable
&& (cmp = ((Comparable) k1).compareTo(k2)) != 0) { // 再次增加一条规则,提高效率
} else if (searched) { // 已经扫描过了
cmp = System.identityHashCode(k1) - System.identityHashCode(k2); // 最后增加一条规则,方便调试,但是不会增加效率
} else { //未扫描,根据内存地址大小决定左右
if ((node.left != null && (result = node(node.left, k1)) != null)
|| (node.right != null && (result = node(node.right, k1)) != null)) {
//已经存在这个key
node = result;
cmp = 0;
} else { // 不存在这个key
searched = true;
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
}
}
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else {
V oldValue = node.value;
node.key = key;//一般覆盖(不同对象可能有相同的比较参数)
node.value = value;
return oldValue;
}
} while (node != null);
// 2.判断插入父节点的左子节点还是右子节点
Node<K, V> newNode = createNode(key, value, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
afterPut(newNode);//新添加节点之后的处理
return null;
}
/**
* 桶数组扩容
*/
private void resize() {
if (size / table.length <= DEFAULT_LOAD_FACTOR) return;
// 扩容
Node<K, V>[] oldTable = table;
table = new Node[table.length << 1];
// 分析:
// 当扩容为原来的两倍时,节点的索引有2种情况
// 1. 保持不变
// 2. index = index + 旧容量
// 层序遍历每个节点开始挪动
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : oldTable) {
if (kvNode == null) continue;
queue.offer(kvNode);
while (!queue.isEmpty()) {
Node<K, V> node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
moveNode(node);
}
}
}
private void moveNode(Node<K, V> newNode) {
// 重置node
newNode.parent = null;
newNode.left = null;
newNode.right = null;
newNode.color = RED;
int index = index(newNode);
// 取出index位置的红黑树根节点
Node<K, V> root = table[index];
if (root == null) {
root = newNode;
table[index] = root;
afterPut(root);
return;
}
// hash冲突,添加新节点到红黑树
// 1.找到待添加位置的父节点
Node<K, V> parent = root;
Node<K, V> node = root;
int cmp = 0;
K k1 = newNode.key;
int h1 = newNode.keyHash;
do {
parent = node;
K k2 = node.key;
int h2 = node.keyHash;
// 增加规则,先比较hash值,提高效率
if (h1 > h2) {
cmp = 1;
} else if (h1 < h2) {
cmp = -1;
} else if (k1 != null && k2 != null
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable
&& (cmp = ((Comparable) k1).compareTo(k2)) != 0) { // 再次增加一条规则,提高效率
} else {
cmp = System.identityHashCode(k1) - System.identityHashCode(k2);
}
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
}
} while (node != null);
// 2.判断插入父节点的左子节点还是右子节点
newNode.parent = parent;
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
afterPut(newNode);//新添加节点之后的处理
}
private void afterPut(Node<K, V> node) {
Node<K, V> parent = node.parent;
//添加的是根节点 或 上溢到根节点
if (parent == null) {
black(node);
return;
}
//类型一:parent是黑色(不用处理四种情况)
if (isBlack(parent)) return;
//类型二:parent是红色且uncle是红色(会上溢的四种情况)
Node<K, V> uncle = parent.getSibling();
Node<K, V> grand = red(parent.parent);//以下情况都需要将grand染成红色,可以统一处理
if (isRed(uncle)) {
black(parent);
black(uncle);
//把祖父节点当作是新添加的节点
afterPut(grand);//上溢递归调用
return;
}
//类型三:parent是红色且uncle不是红色(需要旋转的四种情况)
if (parent.isLeftChild()) {//L
if (node.isLeftChild()) { //LL
black(parent);
} else { //LR
black(node);
rotateLeft(parent);
}
rotateRight(grand);
} else { //R
if (node.isLeftChild()) { //RL
black(node);
rotateRight(parent);
} else { //RR
black(parent);
}
rotateLeft(grand);
}
}
/**
* 给节点上色
*/
private Node<K, V> color(Node<K, V> node, boolean color) {
if (node == null) return node;
node.color = color;
return node;
}
/**
* 将节点染成红色
*/
private Node<K, V> red(Node<K, V> node) {
return color(node, RED);
}
/**
* 将节点染成黑色
*/
private Node<K, V> black(Node<K, V> node) {
return color(node, BLACK);
}
/**
* 获取当前节点的颜色
*/
private boolean colorOf(Node<K, V> node) {
return node == null ? BLACK : node.color;
}
/**
* 判断当前颜色是否为黑色
*/
private boolean isBlack(Node<K, V> node) {
return colorOf(node) == BLACK;
}
/**
* 判断当前颜色是否为红色
*/
private boolean isRed(Node<K, V> node) {
return colorOf(node) == RED;
}
/**
* 左旋转,以RR为例
*/
private void rotateLeft(Node<K, V> grand) {
Node<K, V> parent = grand.right;
Node<K, V> child = parent.left;//child就是T1子树
grand.right = child;
parent.left = grand;
afterRotate(grand, parent, child);
}
/**
* 右旋转,以LL为例
*/
private void rotateRight(Node<K, V> grand) {
Node<K, V> parent = grand.left;
Node<K, V> child = parent.right;
grand.left = child;
parent.right = grand;
afterRotate(grand, parent, child);
}
/**
* 抽取左旋转和右旋转中的重复代码
*/
private void afterRotate(Node<K, V> grand, Node<K, V> parent, Node<K, V> child) {
//更新parent的parent(让parent成为子树的根节点)
parent.parent = grand.parent;
if (grand.isLeftChild()) {
grand.parent.left = parent;
} else if (grand.isRightChild()) {
grand.parent.right = parent;
} else { //grand是root节点
table[index(grand)] = parent;
}
//更新child的parent
if (child != null) {
child.parent = grand;
}
//更新grand的parent
grand.parent = parent;
}
@Override
public V get(K key) {
Node<K, V> node = node(key);
return node != null ? node.value : null;
}
private Node<K, V> node(K key) {
Node<K, V> root = table[index(key)];
return root == null ? null : node(root, key);
}
private Node<K, V> node(Node<K, V> node, K k1) {
int h1 = hash(k1);
// 储存查找结果
Node<K, V> result = null;
int cmp = 0;
while (node != null) {
K k2 = node.key;
int h2 = node.keyHash;
// 增加规则,先比较hash值,提高效率
if (h1 > h2) {
node = node.right;
} else if (h1 < h2) {
node = node.left;
} else if (Objects.equals(k1, k2)) {
return node;
} else if (k1 != null && k2 != null
&& k1.getClass() == k2.getClass()
&& k1 instanceof Comparable
&& (cmp = ((Comparable) k1).compareTo(k2)) != 0) { // 再次增加一条规则,提高效率
node = cmp > 0 ? node.right : node.left;
} else if (node.right != null && (result = node(node.right, k1)) != null) { // 哈希值相等,不具备可比较性,也不equals
return result;
} else { //只能往左边扫
node = node.left;
}
}
return null;
}
@Override
public V remove(K key) {
return remove(node(key));
}
protected V remove(Node<K, V> node) {
if (node == null) return null;
Node<K, V> willNode = node;
size--;
V oldValue = node.value;
//考虑度为2的节点,转化为度为1
if (node.hasTwoChildren()) {
Node<K, V> s = successor(node);//后继节点
//用后继节点的值覆盖度为2的节点的值
node.key = s.key;
node.value = s.value;
node.keyHash = s.keyHash;
//删除后继节点
node = s;
}
//删除node节点(能到这则说明node的度必为0或1)
Node<K, V> replacement = node.left != null ? node.left : node.right;
int index = index(node);
if (replacement != null) { //node是度为1的节点
//更改parent
replacement.parent = node.parent;
//更改parent的left,right指向
if (node.parent == null) { //node是度为1的节点也是根节点
table[index] = replacement;
} else if (node == node.parent.left) {
node.parent.left = replacement;
} else { //在右边
node.parent.right = replacement;
}
//此时开始恢复平衡(AVL树 或 RB树需要实现此方法)
afterRemove(node, replacement);
} else if (node.parent == null) { //node是叶子节点也是根节点
table[index] = null;
afterRemove(node, null);
} else { //node是叶子节点但不是根节点
if (node == node.parent.left) {
node.parent.left = null;
} else {
node.parent.right = null;
}
//此时开始恢复平衡(AVL树 或RB树 需要实现此方法)
afterRemove(node, null);
}
// 交给子类去处理
subclassAfterRemove(willNode, node);
return oldValue;
}
protected void subclassAfterRemove(Node<K, V> willNode, Node<K, V> removedNode) {}
/**
* 实现删除节点后的处理操作
*/
private void afterRemove(Node<K, V> node, Node<K, V> replacement) {
//情况一:如果删除的节点是红色,不用处理
if (isRed(node)) return;
//情况二:用于取代node子节点的是红色节点
if (isRed(replacement)) {
black(replacement);
return;
}
//情况三:删除的是黑色叶子节点(下溢)
Node<K, V> parent = node.parent;
//删除的是根节点
if (parent == null) return;
//判断被删除的node的节点是左还是右
boolean left = parent.left == null || node.isLeftChild();
Node<K, V> sibling = left ? parent.right : parent.left;
if (left) { //被删除的节点在左边,兄弟节点在右边(镜像对称处理)
if (isRed(sibling)) { //兄弟节点是红色,就要转成黑色
black(sibling);
red(parent);
rotateLeft(parent);
//更换兄弟
sibling = parent.right;
}
//兄弟节点必然是黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
//兄弟节点没有一个红色子节点,父节点要向下向子节点合并
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove(parent, null);
}
} else { //兄弟节点至少有 1 个红色节点,就要向兄弟节点借元素
if (isBlack(sibling.right)) {
//兄弟节点的右边不是红色,则兄弟要先旋转
rotateRight(sibling);
sibling = parent.right;
}
color(sibling, colorOf(parent));
black(sibling.right);
black(parent);
rotateLeft(parent);
}
} else { //被删除的节点在右边,兄弟节点在左边(图示的是这种)
if (isRed(sibling)) { //兄弟节点是红色,就要转成黑色
black(sibling);
red(parent);
rotateRight(parent);
//更换兄弟
sibling = parent.left;
}
//兄弟节点必然是黑色
if (isBlack(sibling.left) && isBlack(sibling.right)) {
//兄弟节点没有一个红色子节点,父节点要向下向子节点合并
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove(parent, null);
}
} else { //兄弟节点至少有 1 个红色节点,就要向兄弟节点借元素
if (isBlack(sibling.left)) {
//兄弟节点的左边不是红色,则兄弟要先旋转
rotateLeft(sibling);
sibling = parent.left;
}
color(sibling, colorOf(parent));
black(sibling.left);
black(parent);
rotateRight(parent);
}
}
}
/**
* 利用中序遍历求某个节点的后继节点
*/
private Node<K, V> successor(Node<K, V> node) {
if (node == null) return null;
//前驱节点在右子树中:node.right.left.left...
Node<K, V> p = node.right;
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
//从祖父节点中寻找前驱节点
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
//情况一:node.parent == null ↓
//情况二:node == node.parent.left ↓
return node.parent;
}
@Override
public boolean containsKey(K key) {
return node(key) != null;
}
/**
* 遍历每一个节点的value,红黑树使用层序遍历
*
* @param value 每一个节点的value
* @return bool
*/
@Override
public boolean containsValue(V value) {
if (size == 0) return false;
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
queue.offer(kvNode);
while (!queue.isEmpty()) {
Node<K, V> node = queue.poll();
if (Objects.equals(value, node.value)) return true;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
return false;
}
@Override
public void traversal(Visitor<K, V> visitor) {
if (size == 0 || visitor == null) return;
Queue<Node<K, V>> queue = new LinkedList<>();
for (Node<K, V> kvNode : table) {
if (kvNode == null) continue;
queue.offer(kvNode);
while (!queue.isEmpty()) {
Node<K, V> node = queue.poll();
if (visitor.visit(node.key, node.value)) return;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
}
public void print() {
if (size == 0) return;
for (final Node<K, V> root : table) {
BinaryTrees.println(new BinaryTreeInfo() {
@Override
public Object root() {
return root;
}
@Override
public Object left(Object node) {
return ((Node<K, V>) node).left;
}
@Override
public Object right(Object node) {
return ((Node<K, V>) node).right;
}
@Override
public Object string(Object node) {
return node;
}
});
}
}
}哈希值的进一步处理:扰动计算
在上面的hashmap实现中,生成hash值时为什么还要再次高低16位做与运算?
==> 扰动计算,能使hash排布更加均匀!
private int hash(K key) {
if (key == null) return 0;
int h = key.hashCode();
return (h ^ (h >>> 16)) & (table.length - 1);
}装填因子
在上面的hashmap实现中,在扩容时用到了 装填因子 !
装填因子(Load Factor):节点总数量 / 哈希表桶数组长度,也叫做负载因子
在JDK1.8的HashMap中,如果装填因子超过0.75,就扩容为原来的2倍
关于使用%来计算索引
如果使用%来计算索引
- 建议把哈希表的长度设计为素数(质数),可以大大减小哈希冲突
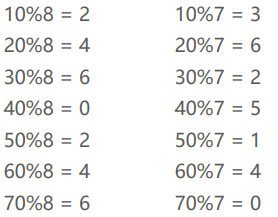
下边表格列出了不同数据规模对应的最佳素数,特点如下
- 每个素数略小于前一个素数的2倍
- 每个素数尽可能接近2的幂(2^n)
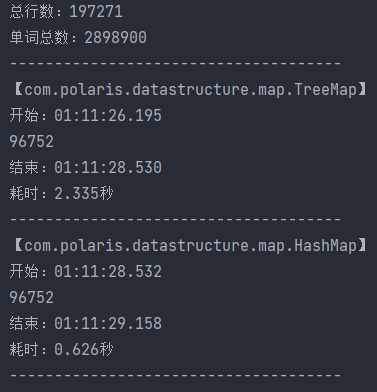
TreeMap VS HashMap
###1 性能对比
###2 选择时机
何时选择 TreeMap? => 元素具备可比较性且要求升序遍历(按照元素从小到大)
何时选择 HashMap?=> 无序遍历
LinkedHashMap
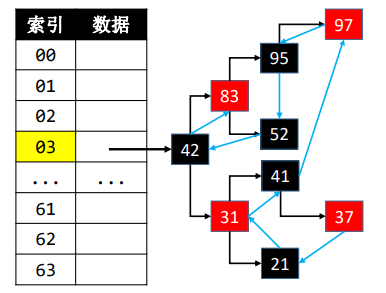
理解
在HashMap的基础上维护元素的添加顺序,使得遍历的结果是遵从添加顺序的
假设添加顺序是:37、21、31、41、97、95、52、42、83
LinkedHashMap实现
/**
* @Description LinkedHashMap, 采取双向链表,提高效率
* @Author monap
* @Date 2022/1/2 15:53
*/
@SuppressWarnings("unchecked")
public class LinkedHashMap<K, V> extends HashMap<K, V> {
private LinkedHashNode<K, V> first;
private LinkedHashNode<K, V> last;
private static class LinkedHashNode<K, V> extends Node<K, V> {
LinkedHashNode<K, V> prev;
LinkedHashNode<K, V> next;
public LinkedHashNode(K key, V value, Node<K, V> parent) {
super(key, value, parent);
}
}
@Override
protected Node<K, V> createNode(K key, V value, Node<K, V> parent) {
LinkedHashNode<K, V> node = new LinkedHashNode<>(key, value, parent);
if (first == null) {
first = last = node;
} else {
last.next = node;
node.prev = last;
last = node;
}
return node;
}
@Override
public void clear() {
super.clear();
first = null;
last = null;
}
@Override
protected void subclassAfterRemove(Node<K, V> willNode,Node<K, V> removedNode) {
LinkedHashNode<K, V> node1 = (LinkedHashNode<K, V>) willNode;
LinkedHashNode<K, V> node2 = (LinkedHashNode<K, V>) removedNode;
if(node1 != node2) {
// 交换linkedHashWillNode和linkedHashRemovedNode在链表中的位置
// 交换prev
LinkedHashNode<K,V> tmp = node1.prev;
node1.prev = node2.prev;
node2.prev = tmp;
if(node1.prev == null) {
first = node1;
} else {
node1.prev.next = node1;
}
if(node2.prev == null) {
first = node2;
} else {
node2.prev.next = node2;
}
//交换last
tmp = node1.next;
node1.next = node2.next;
node2.next = tmp;
if(node1.next == null) {
last = node1;
} else {
node1.next.prev = node1;
}
if(node2.next == null) {
last = node2;
} else {
node2.next.prev = node2;
}
}
LinkedHashNode<K, V> prev = node2.prev;
LinkedHashNode<K, V> next = node2.next;
if (prev == null) {
first = next;
} else {
prev.next = next;
}
if (next == null) {
last = prev;
} else {
next.prev = prev;
}
}
@Override
public boolean containsValue(V value) {
LinkedHashNode<K, V> node = first;
while (node != null) {
if (Objects.equals(value,node.value)) return true;
node = node.next;
}
return false;
}
@Override
public void traversal(Visitor<K, V> visitor) {
if (visitor == null) return;
LinkedHashNode<K, V> node = first;
while (node != null) {
if (visitor.visit(node.key, node.value)) return;
node = node.next;
}
}
}注意:链表是跨红黑树的!
删除的注意点
删除度为2的节点node时(比如删除31),需要注意更换 node 与 前驱\后继节点 的连接位置
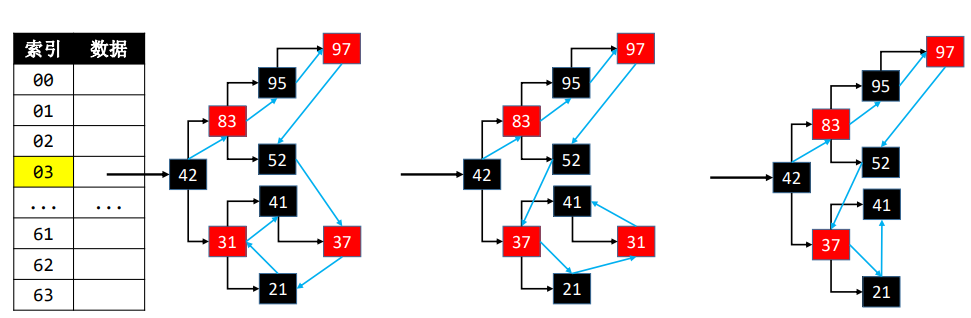
更换节点的连接位置

交换prev
LinkedNode<K,V> tmp = node1.prev;
node1.prev = node2.prev;
node2.prev = tmp;
if (node1.prev != null) {
node1.prev.next = node1;
} else {
first = node1;
}
if (node2.prev != null) {
node2.prev.next = node2;
} else {
first = node2;
}交换next
tmp = node.next;
node1.next = node2.next;
node2.next = tmp;
if (node1.next != null) {
node1.next.prev = node1;
} else {
last = node1;
}
if (node2.next != null) {
node2.next.prev = node2;
} else {
last = node2;
}HashSet
/**
* @Description TODO
* @Author monap
* @Date 2022/1/3 2:25
*/
public class HashSet<E> implements Set<E> {
private HashMap<E,Object> map = new HashMap<>();
@Override
public int size() {
return map.size();
}
@Override
public boolean isEmpty() {
return map.isEmpty();
}
@Override
public void clear() {
map.clear();
}
@Override
public boolean contains(E element) {
return map.containsKey(element);
}
@Override
public void add(E element) {
map.put(element,null);
}
@Override
public void remove(E element) {
map.remove(element);
}
@Override
public void traversal(Visitor<E> visitor) {
map.traversal(new Map.Visitor<E,Object>() {
@Override
public boolean visit(E key, Object value) {
return visitor.visit(key);
}
});
}
}LinkedHashSet
/**
* @Description TODO
* @Author monap
* @Date 2022/1/3 2:25
*/
public class LinkedHashSet<E> implements Set<E> {
private LinkedHashMap<E,Object> map = new LinkedHashMap<>();
@Override
public int size() {
return map.size();
}
@Override
public boolean isEmpty() {
return map.isEmpty();
}
@Override
public void clear() {
map.clear();
}
@Override
public boolean contains(E element) {
return map.containsKey(element);
}
@Override
public void add(E element) {
map.put(element,null);
}
@Override
public void remove(E element) {
map.remove(element);
}
@Override
public void traversal(Visitor<E> visitor) {
map.traversal(new Map.Visitor<E,Object>() {
@Override
public boolean visit(E key, Object value) {
return visitor.visit(key);
}
});
}
}